Tehtävän 16 ratkaisu

Määrätään lukujen 60 ja 84 suurin yhteinen tekijä Eukleideen algoritmilla (ks. s. 22):

Siten syt(60, 84) = 12 = d.

Esitetään suurin yhteinen tekijä lukujen 60 ja 84 monikertasummana eli summana, jossa yhtenä summattavana on luku 60 jollain kokonaislukukertoimella kerrottuna (eli luvun 60 monikerta) ja toisena summattavana vastaavasti luvun 84 monikerta. Monikertasummaesitys voidaan joko koettaa arvata kuten edellisen tehtävän d)-kohdassa tehtiin tai voidaan käyttää nk. paluualgoritmia, joka pohjautuu Eukleideen algoritmiin (ks. s. 24, Esim. II.2.10.). Paluualgoritmia käyttämällä saadaan:

ja näin ollen yhtälön 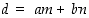kertoimiksi käyvät 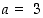ja .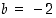

Lisätietoja. Jos ratkaisun tuottavia lukupareja ( a, b) on olemassa yksikin, on niitä tällöin äärettömän paljon kuten tekstissä tämän opiskelutehtävän jälkeen todetaan.

Linkkejä:

Eukleideen algoritmi: http://en.wikipedia.org/wiki/Euclidean_algorithm

Syt: http://en.wikipedia.org/wiki/Greatest_common_divisor

Syt: http://amby.com/educate/math/2-1_GCF.html

[Opiskelutehtävä 16] [Vinkki tehtävään 16]

[Ylempi pääsivu] [Edellinen sivu] [Seuraava sivu]