Tehtävän 3 ratkaisu

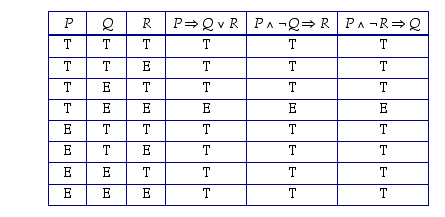
a) Todistus totuustaulun avulla:

Todistus esimerkkiä 1.2.2 ja lausetta 1.2.3 hyödyntäen:

b) "Jaoton kokonaisluku on pariton tai kakkonen" voidaan muuttaa muotoon "Jos kokonaisluku on jaoton, se on pariton tai kakkonen." Väitettä vastaa näin ollen lause 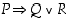, missä P tarkoittaa väitettä "luku on jaoton kokonaisluku", Q väitettä "luku on pariton (kokonaisluku)" ja R väitettä "luku on kakkonen".

Sama asia voidaan a)-kohdassa todetun ekvivalenttiuden nojalla lausua sanallisesti myös näissä kahdessa muodossa:

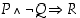: "Jaoton ja parillinen kokonaisluku on kakkonen" tai "Jos kokonaisluku on jaoton ja ei-pariton (siis parillinen), niin se on kakkonen."

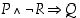: "Jaoton kokonaisluku, joka ei ole kakkonen, on pariton" tai "Jos kokonaisluku on jaoton ja se ei ole kakkonen, niin sen täytyy olla pariton."

[Opiskelutehtävä 2] [Vinkki tehtävään 2]

[Ylempi pääsivu] [Edellinen sivu] [Seuraava sivu]