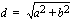
a ) Pisteet sijaitsevat koordinaattiakseleilla, joten niiden etäisyys on muodostuvan suorakulmaisen kolmion hypotenuusan pituus, joka saadaan ratkaistua Pythagoraan lauseen avulla
b ) Pisteen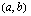 
etäisyyden 
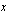-akselista ilmoittaa pisteen 
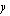-koordinaatti.
Muodostetaan pisteen etäisyyttä suorasta kuvaava funktio, jolle etsitään minimi. Suoran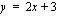 
mielivaltaisen pisteen 
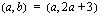etäisyys pisteestä 
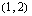on
Pisteen lyhin etäisyys suorasta saadaan etsimällä etäisyysfunktion minimi. Derivoidaan funktio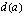 
ja etsitään sen nollakohdat.
Derivaatan (murtofunktio, jonka määrittelyjoukko on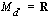 
) nollakohdat saadaan osoittajan nollakohdista 
.
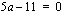Lisätään yhtälön molemmille puolille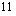 
ja jaetaan muuttujan 
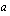kerroin 5 pois.
Derivaatan ainoa nollakohta (ääriarvokohta), jossa funktio saa merkkikaavion perusteella miniminsä (ääriarvo) on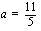 
.
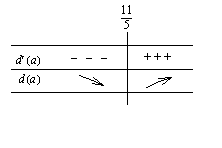
Funktion minimi kohdassa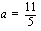 
on (sijoitus kannattaa tehdä alkuperäiseen yhtälöön)
Pisteen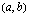 
lyhin etäisyys suorasta on siis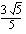 
[Tehtävä 12.1][Vinkki tehtävään 12.1]
