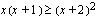Ratkaisu tehtävään 8.1

a ) Sievennetään epäyhtälöä 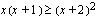kertomalla sulut auki ja laskemalla binomin neliö.

Siirretään ensin kaikki termit epäyhtälön 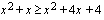oikealle puolelle.

Sieventämisen jälkeen saadaan ensimmäisen asteen epäyhtälö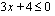

Vähennetään yhtälön molemmilta puolilta 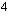ja jaetaan muuttujan 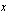kertoimella .

Epäyhtälö toteutuu, kun .

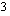b ) Siirretään ensin kaikki termit epäyhtälön 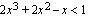vasemmalle puolelle.

Epäyhtälön ratkaisemiseksi etsitään vastaavan yhtälön 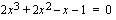juuret ja jaetaan polynomi tekijöihinsä. Mahdolliset rationaaliluku juuret saadaan kokonaislukukertoimiselle yhtälölle vakiotermin ja korkeimman asteen termin tekijöiden suhteena. Nyt ehdokkaita ovat 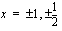. Kokeillaan toteuttaako 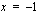yhtälön.

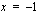toteuttaa yhtälön, joten yhtälöllä on tekijä .

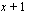Mahdolliset muut juuret saadaan jakamalla polynomi 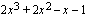tekijällään 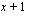jakokulman avulla.

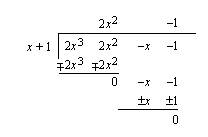
Polynomi voidaan nyt kirjoittaa tekijöidensä tulona summan ja erotuksen muistikaavaa apuna käyttäen (tai ratkaisemalla yhtälö ).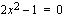

Polynomilla on rationaalijuuri 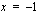ja irrationaalijuuret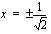

Tehdään merkkikaavio, jonka avulla voidaan tutkia milloin epäyhtälö 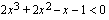on voimassa.

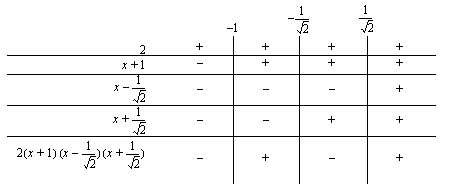
Epäyhtälö on siis voimassa, kun tulo

on negatiivinen eli kun 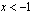.tai .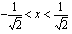

[Tehtävä 8.1][Vinkki tehtävään 8.1]

[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]