Ratkaisu tehtävään 5.3
a ) Juurifunktio 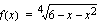 on määritelty, kun juurrettava on suurempi tai yhtäsuuri kuin nolla. Eli kun
on määritelty, kun juurrettava on suurempi tai yhtäsuuri kuin nolla. Eli kun 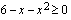 . Epäyhtälöä vastaavan yhtälö
. Epäyhtälöä vastaavan yhtälö 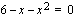 on toisen asteen yhtälö, jonka nollakohdat voidaan ratkaista toisen asteen yhtälön ratkaisukaavalla. Kirjoitetaan vasemman puolen polynomi alenevien potenssien mukaan seuraavasti
on toisen asteen yhtälö, jonka nollakohdat voidaan ratkaista toisen asteen yhtälön ratkaisukaavalla. Kirjoitetaan vasemman puolen polynomi alenevien potenssien mukaan seuraavasti 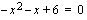 .
.
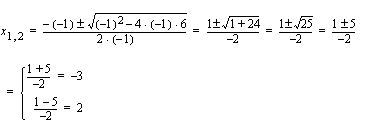
Juurrettavan kuvaaja on alaspäin aukeava paraabeli, joten se saa positiivisia arvoja ainoastaan nollakohtien välissä.
Funktio 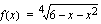 on määritelty, kun
on määritelty, kun 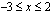 .
.
b ) Funktio
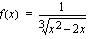
on määritelty, kun nimittäjä on erisuuri kuin nolla. Eli kun 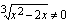 . Juurifunktio on nollasta eroava silloin, kun juurrettava on erisuuri kuin nolla ts.
. Juurifunktio on nollasta eroava silloin, kun juurrettava on erisuuri kuin nolla ts. 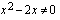 .
.
Yhtälö ratkaistaan ottamalla yhteiseksi tekijäksi 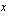 .
.
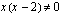
Tulon nollasäännön mukaan tulo on nolla, jos toinen tulon tekijöistä on nolla.
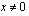 tai
tai 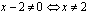
Funktio 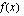 on määritelty, kun
on määritelty, kun 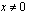 tai
tai 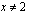 .
.
[Tehtävä 5.3][Vinkki tehtävään 5.3]
[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]
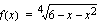 on määritelty, kun juurrettava on suurempi tai yhtäsuuri kuin nolla. Eli kun
on määritelty, kun juurrettava on suurempi tai yhtäsuuri kuin nolla. Eli kun 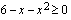 . Epäyhtälöä vastaavan yhtälö
. Epäyhtälöä vastaavan yhtälö 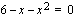 on toisen asteen yhtälö, jonka nollakohdat voidaan ratkaista toisen asteen yhtälön ratkaisukaavalla. Kirjoitetaan vasemman puolen polynomi alenevien potenssien mukaan seuraavasti
on toisen asteen yhtälö, jonka nollakohdat voidaan ratkaista toisen asteen yhtälön ratkaisukaavalla. Kirjoitetaan vasemman puolen polynomi alenevien potenssien mukaan seuraavasti 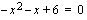 .
.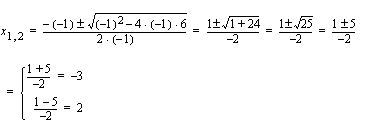
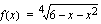 on määritelty, kun
on määritelty, kun 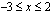 .
.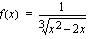
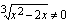 . Juurifunktio on nollasta eroava silloin, kun juurrettava on erisuuri kuin nolla ts.
. Juurifunktio on nollasta eroava silloin, kun juurrettava on erisuuri kuin nolla ts. 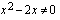 .
.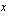 .
.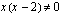
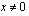 tai
tai 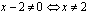
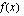 on määritelty, kun
on määritelty, kun 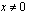 tai
tai 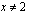 .
.