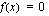.
Määritetään edellisen tehtävän funktion nollakohdat ratkaisemalla yhtälö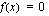
.
Kun funktio on paloittain määritelty, löydetään nollakohdat helposti. Funktiolla on nollakohta ainoastaan välillä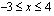 
, jolloin funktio on ensimmäisen asteen polynomi. Muualla funktio on vakiofunktio, eikä sillä ole nollakohtia. Ratkaistaan yhtälö 
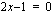funktion nollakohtien löytämiseksi.
Lisätään yhtälön molemmille puolille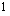 
Jaetaan yhtälön molemmat puolet muuttujan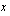 
kertoimella 
.
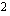Saatu ratkaisu kuuluu määrittelyväliin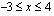 
, joten se käy ratkaisuksi. Funktiolla 
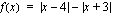on siis yksi nollakohtia 
.
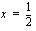Nollakohdat voidaan ratkaista myös suoraan asettamalla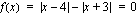 
.
Itseisarvon määritelmän avulla saadaan yhtälö muotoon.
Tarkastellaan tilanteet erikseen:
Vähentämällä molemmilta puolilta yhtälöä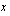 
huomataan, että yhtälö on identtisesti epätosi 
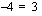, joten sillä ei ole ratkaisua.
Lisätään yhtälön molemmille puolille ´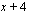
ja sievennetään.
Jaetaan yhtälön molemmat puolet muuttujan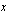 
kertoimella 
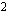, jolloin saadaan sama ratkaisu kuin edellä.
[Tehtävä 4.4][Vinkki tehtävään 4.4]
