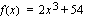Ratkaisu tehtävään 2.1

Ilmoita polynomifunktio 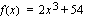tekijöidensä tulona.

Ratkaistaan kolmannen asteen polynomin nollakohdat, jotta se voidaan jakaa tekijöihinsä.

Vähennetään yhtälön molemmilta puolilta 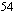ja jaetaan yhtälön molemmat puolet termin 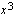kertoimella .

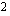Otetaan kuutiojuuri puolittain, jolloin päästään eroon vasemman puolen kuutiosta.

Polynomilla on nollakohta 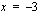, joten eräs sen tekijä on 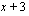. Muut nollakohdat saadaan, kun jaetaan polynomi tekijällään 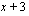jakokulmassa ja ratkaistaan saadun toisen asteen polynomin nollakohdat.

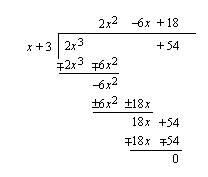
Polynomi voidaan nyt kirjoittaa muodossa 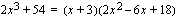. Lasketaan toisen tekijän 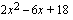nollakohdat toisen asteen yhtälön ratkaisukaavan avulla.

Diskriminantti 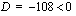, joten ei reaalisia ratkaisuja.

Funktion 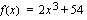tekijät ovat 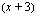ja 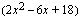, joten funktio voidan kirjoittaa tekijöidensä avulla seuraavasti:

[Tehtävä 2.1][Vinkki tehtävään 2.1]

[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]