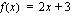Ratkaisu tehtävään 1.9

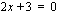a ) Ratkaistaan funktioiden nollakohdat ratkaisemalla seuraavat yhtälöt.

Funktion 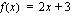nollakohdat saadaan ratkaisemalla yhtälö :

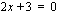Vähennetään yhtälön molemmilta puolilta kolme ja jaetaan yhtälön molemmat puolet kahdella.

Funktion 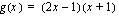nollakohdat saadaan ratkaisemalla yhtälö 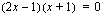. Tulon nollasäännön nojalla joko 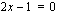tai 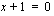. Ensimmäisestä saadaan lisäämällä molemmille puolille yhtälöä 1 ja jakamalla yhtälön molemmat puolet kahdella 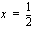ja jälkimmäisestä vähentämällä yhtälön molemmilta puolilta yksi .

Lasketaan yhdistetty funktio:

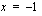Ratkaistaan yhdistetyn funktion nollakohdat.

Tulon nollasäännön nojalla joko 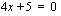tai 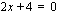. Ensimmäisestä saadaan vähentämällä molemmilta puolilta yhtälöä 5 ja jakamalla yhtälön molemmat puolet neljällä 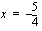ja jälkimmäisestä vähentämällä yhtälön molemmilta puolilta neljä ja jakamalla yhtälön molemmat puolet kahdella .

b ) Funktion nollakohdat:

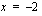Toisen asteen yhtälön ratkaisukaavan avulla saadaan juuret:

Funktion nollakohdat:

Toisen asteen yhtälön ratkaisukaavan avulla saadaan nollakohta:

Lasketaan funktio 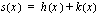ja lasketaan sen nollakohdat:

Funktiolla 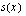ei ole reaalisia nollakohtia, sillä se on aina positiivinen.

[Tehtävä 1.9][Vinkki tehtävään 1.9]

[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]