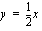 jakaa käyrän
jakaa käyrän 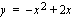 ja
ja 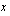 -akselin rajaaman alan kahteen osaan. Lasketaan näiden alojen suhde.
-akselin rajaaman alan kahteen osaan. Lasketaan näiden alojen suhde.
Suora 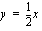 jakaa käyrän
jakaa käyrän 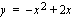 ja
ja 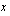 -akselin rajaaman alan kahteen osaan. Lasketaan näiden alojen suhde.
-akselin rajaaman alan kahteen osaan. Lasketaan näiden alojen suhde.
Piirretään ensin tilannetta hahmottava kuva.
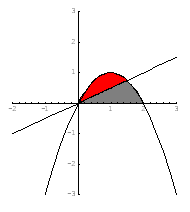
Lasketaan ensin käyrän 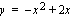 ja
ja 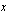 -akselin rajaaman alueen pinta-ala
-akselin rajaaman alueen pinta-ala 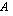 . Laskemalla käyrien rajaamista alueista toisen ala
. Laskemalla käyrien rajaamista alueista toisen ala 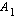 saadaan toisen ala
saadaan toisen ala 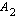 vähentämällä se koko alasta
vähentämällä se koko alasta 
Lasketaan käyrän 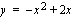 (alaspäin aukeava paraabeli) ja
(alaspäin aukeava paraabeli) ja 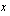 -akselin leikkauskohdat ratkaisemalla yhtälö
-akselin leikkauskohdat ratkaisemalla yhtälö 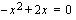 .
.
Yhtälö ratkaistaan ottamalla yhteiseksi tekijäksi 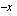 .
.
Tulon nollasäännön mukaan tulo on nolla, jos toinen tulon tekijöistä on nolla.
Paraabelin ja 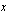 -akselin leikkauspisteet ovat
-akselin leikkauspisteet ovat 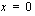 ja
ja 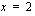 .
.
Lasketaan suoran 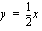 ja käyrän
ja käyrän 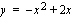 leikkauspisteet ratkaisemalla yhtälöparista muuttuja
leikkauspisteet ratkaisemalla yhtälöparista muuttuja 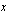 eli integroimiseen tarvittavat leikkauskohdat (integroimisrajat).
eli integroimiseen tarvittavat leikkauskohdat (integroimisrajat).
Sijoitetaan ylemmästä yhtälöstä  :n lauseke alempaan yhtälöön
:n lauseke alempaan yhtälöön 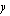 :n paikalle.
:n paikalle.
Siirretään kaikki termit yhtälön vasemmalle puolelle (Muista vaihtaa etumerkit!).
Yhdistetään samanmuotoiset termit.
Yhtälö ratkaistaan ottamalla yhteiseksi tekijäksi 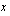 .
.
Tulon nollasäännön mukaan tulo on nolla, jos toinen tulon tekijöistä on nolla.
Suora ja paraabeli leikkavaa kohdissa 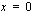 ja
ja 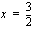 .
.
Tarvittavat tiedot pinta-alojen laskemista varten on määritetty, joten lasketaan alueiden pinta-alat erikseen ja sen jälkeen niiden suhde.
Toisen alueen pinta-ala voidaan laskea myös integroimalla kahdessa osassa.
[Tehtävä 11.5][Vinkki tehtävään 11.5]