[edellinen] [sisällys] [seuraava]
5.1. Matriisi
Tämän luvun opiskeltuasi sinun pitäisi tietää, mikä on matriisi, tuntea matriiseihin liittyvät nimitykset sekä osata matriisien laskutoimitukset. Opiskele asiat luentomonisteen luvusta 2.1. Varmista osaamisesi laskemalla uusiin asioihin liittyvät oppimistehtävät. Tämän luvun vaikein asia on matriisien kertolasku, joka kaivannee hieman lisäselitystä. Opiskele siis lukua omaan tahtiisi aina matriisien kertolaskuun saakka. Luettuasi oheisen yhteenvedon asiasta voit jatkaa monisteen parissa luvun 2.1. loppuun saakka.
Matriisien kertolasku ei ole aina määritelty. Kahden matriisin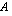 
ja 
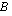tulo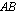 
on määritelty ainoastaan silloin, kun matriisissa 
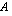on yhtä monta saraketta kuin matriisissa 
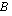on rivejä. Jos esimerkiksi 
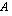on 
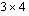-matriisi ja 
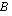on 
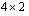-matriisi, on matriisitulo 
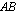määritelty, sillä matriisissa 
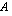on 4 saraketta ja matriisissa 
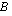on yhtä monta eli 4 riviä. Sen sijaan matriisitulo 
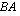ei ole tässä tapauksessa määritelty, koska matriisissa 
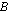on sarakkeita 2, mutta matriisissa 
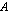on riveja 3. Testaa vielä oheisella testaa tietosi tehtävällä, että osaat päätellä, milloin matriisitulo on määritelty.
Testaa tietosi I
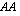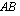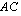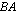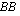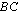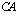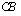Mitkä matriisituloista 
, 
, 
, 
, 
, 
, 
, 
ja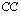 
ovat määriteltyjä?
Olkoon matriisi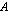 
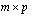-matriisi ja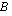 
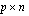-matriisi. Tällöin matriisitulo 
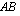on määritelty, koska matriisissa 
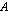on sarakkeita 
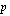kpl eli saman verran kuin matriisissa 
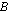on rivejä. Matriisitulo 
muodostetaan kertomalla matriisin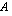 
riveillä matriisin 
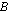sarakkeita seuraavaksi esitettävällä tavalla. Sarakkeen kertominen rivillä tarkoittaa tässä sitä, että kerrotaan rivin ja sarakkeen vastinalkiot keskenään ja lasketaan näin saadut tulot yhteen. Rivin ja sarakkeen ensimmäiset alkiot kerrotaan siis keskenään, sitten toiset alkiot jne. niin kauan kuin alkioita riittää. Alkioita on 
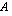:n riveillä ja 
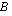:n sarakkeilla aina yhtä monta (tässä 
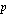kpl) matriisitulon määrittelyehdosta johtuen.
Matriisien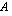 
ja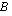 
tulomatriisi 
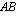muodostetaan seuraavasti: Tulomatriisin 
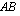ensimmäisen rivin ensimmäinen alkio saadaan kertomalla matriisin 
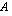ensimmäisellä rivillä matriisin 
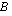ensimmäinen sarake, 
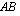:n ensimmäisen rivin toinen alkio saadaan puolestaan kertomalla matriisin 
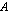ensimmäisellä rivillä matriisin 
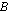toinen sarake. Näin jatketaan niin kauan kuin matriisissa 
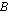riittää kerrottavia sarakkeita. Tulomatriisin 
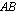toinen rivi muodostuu kertomalla matriisin 
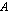toisella rivillä ensin matriisin 
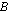ensimmäinen sarake, sitten toinen sarake jne. jälleen niin kauan kuin sarakkeita riittää. Näin jatketaan kertomalla matriisin 
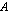kullakin rivillä vuorotellen jokainen matriisin 
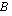sarake. Tulomatriisin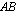 
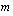:nnen rivin 
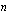:s alkio muodostuu aina kertomalla matriisin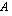 
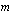:nnellä rivillä matriisin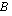 
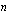:s sarake.
Kun matriisi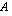 
on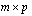 
-matriisi ja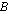 
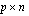-matriisi, on matriisitulo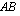 
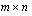-matriisi. Tämä on helppo päätellä edellä esitellystä kertolaskutavasta: koska tulomatriisia varten kerrotaan kaikilla matriisin 
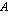riveillä vuorotellen kukin matriisin 
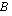sarake, on tulomatriisissa 
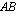oltava rivejä yhtä monta kuin matriisissa 
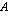ja sarakkeita yhtä monta kuin matriisissa 
.
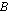Lue nyt, mitä luentomonisteessa kerrotaan matriisien kertolaskusta. Katso erityisesti esmerkki 2.7 ja harjoittele itse matriisien kertolaskua oppimistehtävän 2.8 avulla. Lue vielä lopuksi matriisien kertolaskun ominaisuuksista sekä katso esimerkistä 2.10, kuinka matriisioperaatioita voidaan käyttää kätevästi taulukkotiedon käsittelyyn. Tätä taitoa voit lisäksi harjoitella oppimistehtävän 2.11 avulla.
Selvitä vielä lopuksi, mitä tarkoitetaan matriisin transpoosilla. Tämän jälkeen voit testata oheisella testaa tietosi -tehtävällä, oletko oppinut matriisien laskutoimitukset.
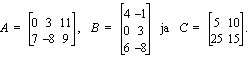
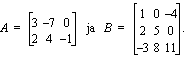
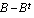(b) 