[edellinen] [sisällys] [seuraava]
4.3. Derivaatta
Derivaatta on apuväline, jota voidaan käyttää mm. funktion kasvamisen ja vähenemisen tutkimiseen sekä funktion paikallisten ääriarvojen - maksimien ja minimien - etsimiseen. Tässä luvussa selvitämme itse derivaattakäsitettä sekä opettelemme määrittämään funktion derivaatan. Seuraavassa luvussa tutustumme joihinkin derivaatan sovelluksiin, kuten edellä mainittuihin funktion monotonisuuden ja ääriarvojen tutkimiseen.
4.3.1. Funktion kasvunopeus
Ohessa on erään funktion 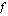 kuvaaja. Tarkastellaan seuraavaa ongelmaa: mikä on funktion
kuvaaja. Tarkastellaan seuraavaa ongelmaa: mikä on funktion 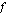 arvojen hetkellinen kasvunopeus kohdassa
arvojen hetkellinen kasvunopeus kohdassa 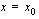 ?
?
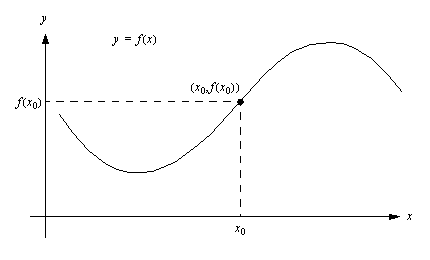
Voimme vaikka ajatella, että muuttuja 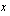 esittää tässä aikaa ja funktio
esittää tässä aikaa ja funktio 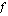 ilmoittaa kappaleen tietyssä ajassa kulkeman matkan. Kuinka sitten määritettäisiin tämän funktion hetkellinen kasvunopeus kohdassa
ilmoittaa kappaleen tietyssä ajassa kulkeman matkan. Kuinka sitten määritettäisiin tämän funktion hetkellinen kasvunopeus kohdassa 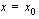 tai vastaavasti jonkun kappaleen hetkellinen nopeus ajanhetkellä
tai vastaavasti jonkun kappaleen hetkellinen nopeus ajanhetkellä 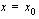 ? Osaamme toki määrittää kappaleen keskinopeuden tietyllä aikavälillä, mutta hetkellisen nopeuden määrittäminen onkin jo hankalampaa.
? Osaamme toki määrittää kappaleen keskinopeuden tietyllä aikavälillä, mutta hetkellisen nopeuden määrittäminen onkin jo hankalampaa.
Lähdetään siis liikkeelle yksinkertaisemmasta ongelmasta: määritetään aluksi funktion keskimääräinen kasvunopeus välillä 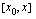 . Tämä tapahtuu samalla tavoin kuin määrittäisimme jonkun kappaleen keskinopeuden aikavälillä
. Tämä tapahtuu samalla tavoin kuin määrittäisimme jonkun kappaleen keskinopeuden aikavälillä 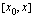 . Kappaleen keskinopeushan lasketaan jakamalla kappaleen kulkema matka siihen käytetyllä ajalla. Ajattelemme nyt funktion
. Kappaleen keskinopeushan lasketaan jakamalla kappaleen kulkema matka siihen käytetyllä ajalla. Ajattelemme nyt funktion 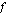 esittävän kappaleen kulkemaa matkaa ja muuttujan
esittävän kappaleen kulkemaa matkaa ja muuttujan 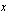 aikaa, jonka kuluessa kyseinen matka on kuljettu. Kappaleen aikavälillä
aikaa, jonka kuluessa kyseinen matka on kuljettu. Kappaleen aikavälillä 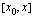 kulkema matka on tällöin erotus
kulkema matka on tällöin erotus 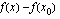 ja matkaan käytetty aika
ja matkaan käytetty aika 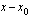 . Kappaleen keskinopeus aikavälillä
. Kappaleen keskinopeus aikavälillä 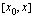 on siis
on siis
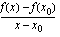 .
.
Tämä on myös funktion 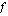 arvojen keskimääräinen kasvunopeus välillä
arvojen keskimääräinen kasvunopeus välillä 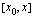 , sillä voimme ajatella, että yleisessä tapauksessa kappaleen kulkemaa matkaa vastaa funktion arvojen muutos kyseisellä välillä ja kappaleen käyttämää aikaa puolestaan vastaa muuttujan arvojen muutos.
, sillä voimme ajatella, että yleisessä tapauksessa kappaleen kulkemaa matkaa vastaa funktion arvojen muutos kyseisellä välillä ja kappaleen käyttämää aikaa puolestaan vastaa muuttujan arvojen muutos.
Palataanpa tarkastelemaan asiaa vielä graafisesti ennen kuin jatkamme varsinaiseen ongelmaamme eli hetkellisen nopeuden määrittämiseen. Valitaan jokin muuttujan arvo 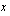 päätepisteeksi välille
päätepisteeksi välille 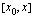 , jolla funktion arvojen keskimmääräistä muutosnopeutta lasketaan. Tätä muuttujan arvoa vastaa kuvaajan piste
, jolla funktion arvojen keskimmääräistä muutosnopeutta lasketaan. Tätä muuttujan arvoa vastaa kuvaajan piste 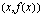 .
.
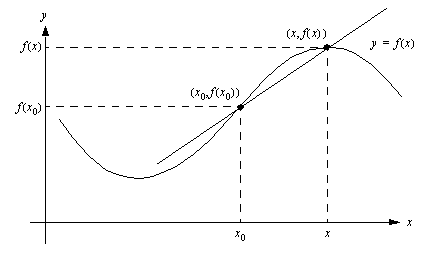
Erotus 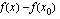 esittää funktion kuvaajan pisteiden
esittää funktion kuvaajan pisteiden 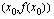 ja
ja 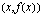
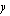 -koordinaattien erotusta ja erotus
-koordinaattien erotusta ja erotus 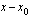 puolestaan niiden
puolestaan niiden 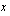 -koordinaattien erotusta. Näiden osamäärä
-koordinaattien erotusta. Näiden osamäärä
on siten pisteiden 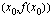 ja
ja 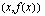 kautta kulkevan suoran kulmakerroin. Tällaista suoraa, joka kulkee kahden kuvaajan pisteen kautta nimitetään funktion kuvaajan sekantiksi. Funktion keskimääräinen kasvunopeus välillä
kautta kulkevan suoran kulmakerroin. Tällaista suoraa, joka kulkee kahden kuvaajan pisteen kautta nimitetään funktion kuvaajan sekantiksi. Funktion keskimääräinen kasvunopeus välillä 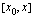 voidaan tämän nojalla tulkita geometrisesti funktion kuvaajan pisteiden
voidaan tämän nojalla tulkita geometrisesti funktion kuvaajan pisteiden 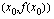 ja
ja 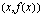 kautta kulkevan sekantin kulmakertoimeksi.
kautta kulkevan sekantin kulmakertoimeksi.
Näin määritimme funktion arvojen keskimääärisen kasvunopeuden tietyllä välillä, mutta kuinka määrittäisimme funktion arvojen hetkellisen kasvunopeuden kohdassa 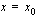 ? Funktion keskimääräinen kasvunopeus välillä
? Funktion keskimääräinen kasvunopeus välillä 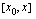 voidaan ajatella arvioksi sen hetkelliselle kasvunopeudelle kohdassa
voidaan ajatella arvioksi sen hetkelliselle kasvunopeudelle kohdassa 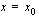 . Tuo arvio paranee, kun pienennetään väliä
. Tuo arvio paranee, kun pienennetään väliä 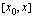 , jolla keskimääärinen nopeus on laskettu. Mitä pienempi tuo väli on sitä paremman arvion hetkelliselle kasvunopeudelle saamme. Välin
, jolla keskimääärinen nopeus on laskettu. Mitä pienempi tuo väli on sitä paremman arvion hetkelliselle kasvunopeudelle saamme. Välin 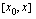 pienentäminen merkitsee sitä, että piste
pienentäminen merkitsee sitä, että piste 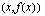 siirtyy lähemmäksi pistettä
siirtyy lähemmäksi pistettä 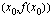 . Alla olevaan kuvioon on piirretty useita eri sekantteja, joiden kulmakertoimien avulla voidaan arvioida funktion hetkellistä kasvunopeutta kohdassa
. Alla olevaan kuvioon on piirretty useita eri sekantteja, joiden kulmakertoimien avulla voidaan arvioida funktion hetkellistä kasvunopeutta kohdassa 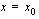 .
.
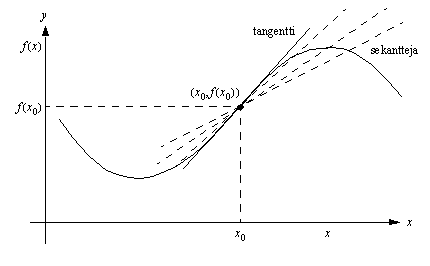
Kun hetkellisen kasvunopeuden arviointia jatketaan tällä tavalla, päädytään lopulta tilanteeseen, jossa väli 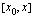 on kutistunut olemattomaksi ja piste
on kutistunut olemattomaksi ja piste 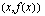 yhtynyt pisteeseen
yhtynyt pisteeseen 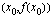 . Tällöin sekantista, jonka kulmakerroin esittää funktion keskimääräistä kasvunopeutta, on tullut funktion kuvaajan tangentti eli sivuaja. Tämän tangentin kulmakerroin ilmaisee funktion hetkellisen kasvunopeuden kohdassa
. Tällöin sekantista, jonka kulmakerroin esittää funktion keskimääräistä kasvunopeutta, on tullut funktion kuvaajan tangentti eli sivuaja. Tämän tangentin kulmakerroin ilmaisee funktion hetkellisen kasvunopeuden kohdassa 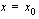 . Laskemalla tuon tangentin kulmakerroin saadaan raja-arvona sekantin kulmakertoimesta. Sekantin kulmakerroin eli funktion keskimääärinen kasvunopeus
. Laskemalla tuon tangentin kulmakerroin saadaan raja-arvona sekantin kulmakertoimesta. Sekantin kulmakerroin eli funktion keskimääärinen kasvunopeus
4.3.2. Derivaatta
Johdimme edellä itse asiassa määritelmän funktion 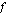 derivaatalle kohdassa
derivaatalle kohdassa 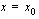 . Funktion
. Funktion 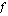 derivaatta kohdassa
derivaatta kohdassa 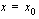 on raja-arvo
on raja-arvo
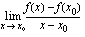 ,
,
jos tämä raja-arvo on olemassa. Funktion derivaatalle kohdassa 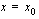 käytetään merkintää
käytetään merkintää 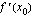 . Funktion derivaatta
. Funktion derivaatta 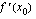 voidaan tulkita funktion
voidaan tulkita funktion 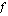 hetkelliseksi kasvunopeudeksi kohdassa
hetkelliseksi kasvunopeudeksi kohdassa 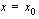 tai funktion
tai funktion 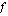 kuvaajan pisteeseen
kuvaajan pisteeseen 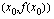 piirretyn tangentin kulmakertoimeksi.
piirretyn tangentin kulmakertoimeksi.
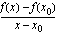 ,
,
jonka raja-arvona funktion derivaatta saadaan, kutsutaan funktion 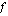 erotusosamääräksi kohdassa
erotusosamääräksi kohdassa 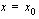 . Tämä erotusosamäärä ilmoittaa funktion
. Tämä erotusosamäärä ilmoittaa funktion 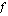 kuvaajan pisteiden
kuvaajan pisteiden 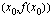 ja
ja 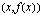 kautta kulkevan sekantin kulmakertoimen.
kautta kulkevan sekantin kulmakertoimen.
Jos edellä mainitulla erotusosamäärällä ei ole raja-arvoa, kun 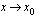 , ei funktio
, ei funktio 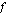 ole derivoituva kohdassa
ole derivoituva kohdassa 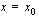 . Näin käy tilanteissa, joita on havainnollistettu kuvin luentomonisteen sivulla 142. Lue tämä sivu aina esimerkkiin 5.12 saakka. Tämän jälkeen voit testata oheisilla testaa tietosi -tehtävillä, oletko ymmärtänyt derivaatan käsitteen.
. Näin käy tilanteissa, joita on havainnollistettu kuvin luentomonisteen sivulla 142. Lue tämä sivu aina esimerkkiin 5.12 saakka. Tämän jälkeen voit testata oheisilla testaa tietosi -tehtävillä, oletko ymmärtänyt derivaatan käsitteen.
Testaa tietosi II
Ohessa on erään funktion 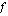 kuvaaja. Vastaa kuvan perusteella seuraaviin kysymyksiin.
kuvaaja. Vastaa kuvan perusteella seuraaviin kysymyksiin.
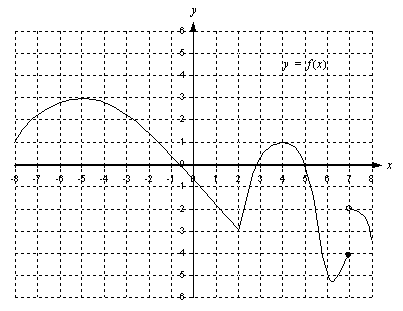
(b) Arvioi kuvaajalta itse piirtämäsi tangentin avulla, mitä on 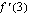 .
.
(d) Kuinka monessa kohdassa 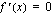 ? Arvioi kuvaajalta nämä kohdat.
? Arvioi kuvaajalta nämä kohdat.
Testaa tietosi III
http://www.cc.jyu.fi/~anvihola/testit/testaa/derivtesti1.php
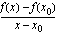
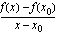
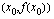 piirretyn tangentin kulmakertoimelle mitä lähempänä
piirretyn tangentin kulmakertoimelle mitä lähempänä 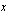 on kohtaa
on kohtaa 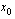 . Funktion hetkellinen kasvunopeus kohdassa
. Funktion hetkellinen kasvunopeus kohdassa 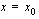 on siten raja-arvo
on siten raja-arvo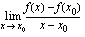 ,
,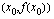 piirretyn tangentin kulmakerroin.
piirretyn tangentin kulmakerroin. 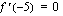 ?
? 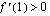 ?
?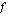 ei ole derivoituva?
ei ole derivoituva?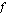 derivaattafunktio on funktio
derivaattafunktio on funktio 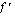 , jonka arvo jokaisessa kohdassa on funktion
, jonka arvo jokaisessa kohdassa on funktion 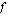 derivaatta tässä kohdassa. Funktion derivaattafunktion muodostamista nimitetään funktion derivoimiseksi. Tällä kurssilla käytämme yleensä funktion
derivaatta tässä kohdassa. Funktion derivaattafunktion muodostamista nimitetään funktion derivoimiseksi. Tällä kurssilla käytämme yleensä funktion 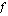 derivaattafunktiolle merkintää
derivaattafunktiolle merkintää 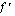 , mutta sitä voidaan myös merkitä seuraavasti:
, mutta sitä voidaan myös merkitä seuraavasti: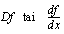 .
. 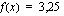 ;
; 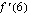
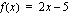 ;
; 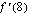
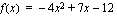 ;
; 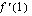
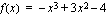 ;
; 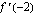
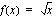 ,
, 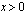 ;
; 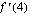
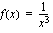 ,
, 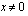 ;
; 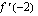
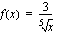 ,
, 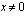 ;
; 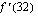
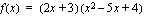 derivaatta
derivaatta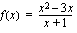 ,
, 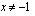
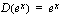 eli eksponenttifunktion
eli eksponenttifunktion 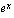 derivaatta on funktio itse ja
derivaatta on funktio itse ja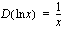 , kun
, kun 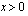 .
.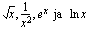 ,
,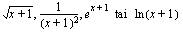 ,
,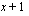 ja ulkofunktiona jokin edellä mainituista perusfunktioista.
ja ulkofunktiona jokin edellä mainituista perusfunktioista. 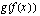 , missä
, missä 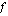 on sisäfunktio ja
on sisäfunktio ja 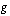 ulkofunktio. Yhdistetyn funktion
ulkofunktio. Yhdistetyn funktion 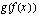 derivaatta on tällöin
derivaatta on tällöin 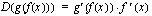 .
.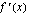 . Toinen tekijä on itsessään yhdistetty funktio, jonka sisäfunktio on sama kuin alkuperäisen funktion sisäfunktio
. Toinen tekijä on itsessään yhdistetty funktio, jonka sisäfunktio on sama kuin alkuperäisen funktion sisäfunktio 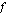 ja ulkofunktio on alkuperäisen ulkofunktion derivaatta
ja ulkofunktio on alkuperäisen ulkofunktion derivaatta 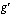 . Tämä toinen tekijä muodostetaan sijoittamalla alkuperäisen ulkofunktion
. Tämä toinen tekijä muodostetaan sijoittamalla alkuperäisen ulkofunktion 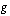 derivaatan
derivaatan 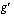 lausekkeeseen muuttujan paikalle sisäfunktion
lausekkeeseen muuttujan paikalle sisäfunktion 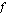 lauseke. Harjoitellaan yhdistetyn funktion derivoimista vaihe vaiheelta seuraavan esimerkin avulla.
lauseke. Harjoitellaan yhdistetyn funktion derivoimista vaihe vaiheelta seuraavan esimerkin avulla. 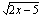 ,
, 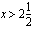 (b)
(b) 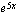 (c)
(c) 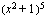
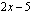 ja ulkofunktio
ja ulkofunktio 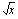 . (Yhdistetyssä funktiossa ulkofunktiota sovelletaan aina koko sisäfunktion lausekkeeseen, tässä sisäfunktiosta
. (Yhdistetyssä funktiossa ulkofunktiota sovelletaan aina koko sisäfunktion lausekkeeseen, tässä sisäfunktiosta 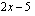 otetaan neliöjuuri.) Tämän yhdistetyn funktion derivaatta on tulo, jonka toinen tekijä on sisäfunktion derivaatta. Tässä tapauksessa sisäfunktion derivaatta on vakio 2. Toinen tämän yhdistetyn funktion derivaatan tekijä saadaan sijoittamalla ulkofunktion
otetaan neliöjuuri.) Tämän yhdistetyn funktion derivaatta on tulo, jonka toinen tekijä on sisäfunktion derivaatta. Tässä tapauksessa sisäfunktion derivaatta on vakio 2. Toinen tämän yhdistetyn funktion derivaatan tekijä saadaan sijoittamalla ulkofunktion 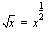 derivaattaan muuttujan paikalle sisäfunktion
derivaattaan muuttujan paikalle sisäfunktion 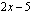 lauseke. Neliöjuurifunktion
lauseke. Neliöjuurifunktion 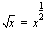 derivaatta on
derivaatta on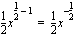 .
.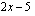 lauseke, saadaan
lauseke, saadaan 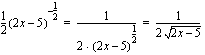 .
.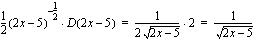 .
.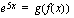 , missä sisäfunktio
, missä sisäfunktio 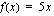 ja ulkofunktio
ja ulkofunktio 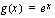 . Tällöin sisäfunktion derivaatta
. Tällöin sisäfunktion derivaatta 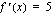 , ulkofunktion derivaatta
, ulkofunktion derivaatta 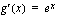 ja yhdistetyn funktion derivaatan toinen tekijä
ja yhdistetyn funktion derivaatan toinen tekijä 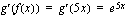 . Funktion derivaatta on tällöin
. Funktion derivaatta on tällöin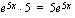 .
. 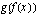 siten, että ulkofunktio
siten, että ulkofunktio 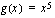 ja sisäfunktio
ja sisäfunktio 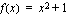 . Funktion derivaatta on nyt yhdistetyn funktion derivoimissääntöä soveltaen
. Funktion derivaatta on nyt yhdistetyn funktion derivoimissääntöä soveltaen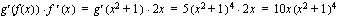 .
.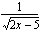 ,
, 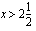
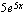
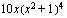
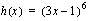 (b)
(b) 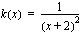 ,
, 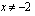
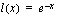 (d)
(d)