(a) Funktio 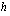 voidaan nyt ajatella yhdistyksi funktioksi
voidaan nyt ajatella yhdistyksi funktioksi 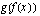 siten, että sisäfunktio
siten, että sisäfunktio 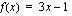 ja ulkofunktio
ja ulkofunktio 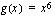 . Yhdistetyn funktion derivoimissääntöä soveltaen saadaan funktion derivaataksi
. Yhdistetyn funktion derivoimissääntöä soveltaen saadaan funktion derivaataksi
(a) Funktio 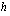 voidaan nyt ajatella yhdistyksi funktioksi
voidaan nyt ajatella yhdistyksi funktioksi 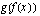 siten, että sisäfunktio
siten, että sisäfunktio 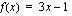 ja ulkofunktio
ja ulkofunktio 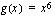 . Yhdistetyn funktion derivoimissääntöä soveltaen saadaan funktion derivaataksi
. Yhdistetyn funktion derivoimissääntöä soveltaen saadaan funktion derivaataksi
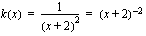 ,
,
joten 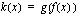 , missä sisäfunktio
, missä sisäfunktio 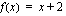 ja ulkofunktio
ja ulkofunktio 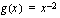 . Nyt sisäfunktion derivaatta
. Nyt sisäfunktion derivaatta 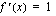 ja yhdistetyn funktion derivaatan toinen tekijä
ja yhdistetyn funktion derivaatan toinen tekijä
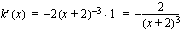 ,
, 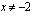 .
.
(c) Funktio 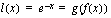 , missä sisäfunktio
, missä sisäfunktio 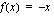 ja ulkofunktio
ja ulkofunktio 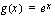 . Yhdistetyn funktion derivoimissäännöllä saadaan
. Yhdistetyn funktion derivoimissäännöllä saadaan