[edellinen] [sisällys] [seuraava]
4.1. Raja-arvo
Aloitetaan tarkastelemalla oheista johdantoesimerkkiä.
Esimerkki 3.1.
Tarkastellaan rationaalifunktiota
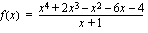 ,
, 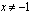 .
.
Tämä funktio ei ole määritelty nimittäjän nollakohdassa 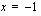 . Funktio on kuitenkin määritelty kaikkialla tämän kohdan läheisyydessä. Tutki, mitä funktion
. Funktio on kuitenkin määritelty kaikkialla tämän kohdan läheisyydessä. Tutki, mitä funktion 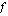 arvoille tapahtuu, kun muuttujan
arvoille tapahtuu, kun muuttujan 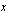 arvot lähestyvät kohtaa
arvot lähestyvät kohtaa 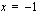 ?
?
Koska johdantoesimerkissämme funktion 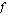 arvot lähestyivät lukua -2, kun muuttujan
arvot lähestyivät lukua -2, kun muuttujan 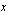 arvot lähestyivät kohtaa
arvot lähestyivät kohtaa 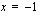 sekä oikealta että vasemmalta, sanotaan, että funktion
sekä oikealta että vasemmalta, sanotaan, että funktion 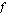 raja-arvo kohdassa
raja-arvo kohdassa 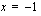 on -2. Tätä voidaan merkitä kahdella eri tavalla:
on -2. Tätä voidaan merkitä kahdella eri tavalla:
Jälkimmäinen merkintä luetaan: "limes 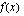 , kun
, kun 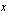 lähestyy lukua -1, on -2". Merkinnän lyhenne lim tulee latinan kielen sanasta limes, joka tarkoittaa rajaa.
lähestyy lukua -1, on -2". Merkinnän lyhenne lim tulee latinan kielen sanasta limes, joka tarkoittaa rajaa.
Funktiolla 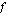 sanotaan olevan kohdassa
sanotaan olevan kohdassa 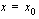 raja-arvo
raja-arvo 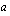 , jos funktion arvot
, jos funktion arvot 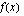 tulevat miten tahansa lähelle lukua
tulevat miten tahansa lähelle lukua 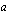 , kun muuttujan
, kun muuttujan 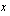 arvot ovat riittävän lähellä lukua
arvot ovat riittävän lähellä lukua 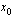 . Sitä, että funktion
. Sitä, että funktion 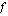 raja-arvo kohdassa
raja-arvo kohdassa 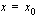 on
on 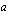 , voidaan merkitä kahdella eri tavalla: joko
, voidaan merkitä kahdella eri tavalla: joko
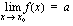 .
.
Lue sitten matematiikan peopedeuttisen kurssin luentomonisteen luvusta 5.1, mitä siellä on kerrottu funktion raja-arvosta. Erityisesti sinun on syytä huomata, että funktion raja-arvo kertoo funktion käyttäytymisestä tarkastelukohdan läheisyydessä, mutta se ei kerro mitään funktion arvosta kyseisessä kohdassa. Katso huolella luentomonisteen kuvat sivulta 129. Kaikissa kuvien esittämissä tilanteissa funktiolla on sama raja-arvo kohdassa 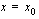 , mutta kyseisessä kohdassa funktio käyttäytyy eri tavalla kaikissa eri tilanteissa. Lue monisteesta myös huomautus, jossa puhutaan funktion vasemman- ja oikeanpuoleisista raja-arvoista. Raja-arvon laskemiseen liittyvät esimerkit voit sivuuttaa, sillä tällä kurssilla tyydymme tarkastelemaan raja-arvon käsitettä ainoastaan funktioiden kuvaajien avulla. Raja-arvon laskemiseen liityville tekniikoille meillä ei ole jatkossa käyttöä, joten niiden opiskelun jätän vapaaehtoiseksi.
, mutta kyseisessä kohdassa funktio käyttäytyy eri tavalla kaikissa eri tilanteissa. Lue monisteesta myös huomautus, jossa puhutaan funktion vasemman- ja oikeanpuoleisista raja-arvoista. Raja-arvon laskemiseen liittyvät esimerkit voit sivuuttaa, sillä tällä kurssilla tyydymme tarkastelemaan raja-arvon käsitettä ainoastaan funktioiden kuvaajien avulla. Raja-arvon laskemiseen liityville tekniikoille meillä ei ole jatkossa käyttöä, joten niiden opiskelun jätän vapaaehtoiseksi.
Luettuasi raja-arvon käsitettä esittelevät kohdat luentomonisteesta voit vielä tarkistaa oheisella testaa tietosi -tehtävällä, olitko ymmärtänyt asian.
Testaa tietosi I
http://www.cc.jyu.fi/~anvihola/testit/testaa/raja_arvo.php
Huom! Palataan vielä hetkeksi johdantoesimerkkiimme 3.1. Siinä esiintyi rationaalifunktio
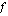 arvoja kohdan
arvoja kohdan 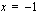 molemmin puolin.
molemmin puolin. 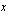
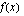
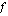 arvot lähestyvät lukua -2, kun muuttujan
arvot lähestyvät lukua -2, kun muuttujan 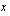 arvot lähestyvät nimittäjän nollakohtaa
arvot lähestyvät nimittäjän nollakohtaa 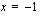 . Sama ilmenee myös oheisesta funktion
. Sama ilmenee myös oheisesta funktion 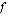 kuvaajasta.
kuvaajasta. 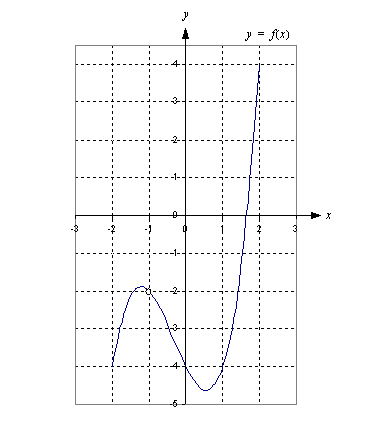
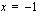 sekä oikealta että vasemmalta, lähestyvät funktion
sekä oikealta että vasemmalta, lähestyvät funktion 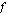 arvot lukua -2.
arvot lukua -2. 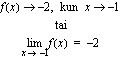
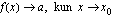
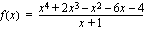 ,
, 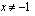 .
. 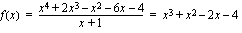 ,
, 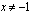 .
.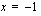 , koska funktiota ei ole määritelty tässä kohdassa.
, koska funktiota ei ole määritelty tässä kohdassa. 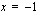 :
: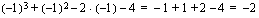 .
. 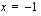 seuraavasti:
seuraavasti: 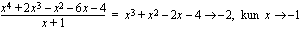 .
.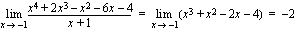 .
.