[edellinen] [sisällys] [seuraava]
3.2. Potenssi- ja juurifunktio
Tutustuimme potenssin ja neliöjuuren käsitteisiin jo kurssin ensimmäisessä modulissa. Tuolloin potenssi määriteltiin niin, että eksponenttina oli jokin positiivinen kokonaisluku. Tässä luvussa laajennamme potenssikäsitettä niin, että eksponenttina voi itse asiassa olla mikä tahansa reaaliluku. Samalla opimme, kuinka esimerkiksi neliöjuuri voidaan ajatella potenssina.
3.2.1. Potenssifunktio
Lue aluksi luentomonisteen luvusta 4.5.1, mitä siellä kerrotaan meille jo tutusta potenssifunktiosta, jossa eksponenttina on jokin positiivinen kokonaisluku. Katso erityisesti potenssifunktion kuvaajia sekä parillisen että parittoman eksponentin tapauksessa. Seuraavalla testaa tietosi -tehtävällä voit varmistaa, että olet havainnut kuvista kaiken oleellisen.
Testaa tietosi II
Vastaa perustellusti seuraaviin kysymyksiin.
(a) Minkä pisteiden kautta funktion 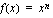 kuvaaja aina kulkee, kun
kuvaaja aina kulkee, kun
(i) 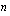 on parillinen? (ii)
on parillinen? (ii) 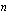 on pariton?
on pariton?
(b) Kuinka monta ratkaisua on yhtälöllä 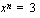 , kun
, kun
(i) 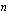 on parillinen? (ii)
on parillinen? (ii) 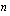 on pariton?
on pariton?
(c) Tiedämme, että reaaliluvulle 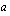 on voimassa
on voimassa 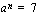 . Ratkaise yhtälö
. Ratkaise yhtälö 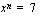 , kun
, kun
(i) 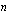 on parillinen (ii)
on parillinen (ii) 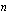 on pariton
on pariton
3.2.2. Juurifunktio
Aloita lukemalla luentomonisteen luvusta 4.5.2 yleisten juurien määritelmistä aina esimerkkiin 4.9 saakka. Tämän luettuasi sinun pitäisi tietää, että reaaliluvun 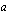
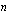 :s juuri, jota merkitään
:s juuri, jota merkitään 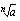 toteuttaa aina ehdon
toteuttaa aina ehdon 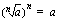 eli luvun
eli luvun 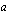
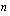 :s juuri on sellainen reaaliluku, joka korotettuna juuren indeksin osoittamaan potenssiin
:s juuri on sellainen reaaliluku, joka korotettuna juuren indeksin osoittamaan potenssiin 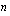 antaa kyseisen luvun
antaa kyseisen luvun 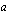 . Mikäli
. Mikäli 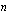 on parillinen eli on kyse ns. parillisesta juuresta, on lisäksi huomattava, että parillinen juuri on määritelty ainoastaan ei-negatiivisille luvuille eli silloin, kun juurrettava
on parillinen eli on kyse ns. parillisesta juuresta, on lisäksi huomattava, että parillinen juuri on määritelty ainoastaan ei-negatiivisille luvuille eli silloin, kun juurrettava 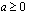 . Lisäksi parillisen juuren arvo on aina ei-negatiivinen. Jos
. Lisäksi parillisen juuren arvo on aina ei-negatiivinen. Jos 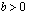 ja
ja 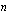 parillinen, on kaksi eri lukua, jotka toteuttavat yhtälön
parillinen, on kaksi eri lukua, jotka toteuttavat yhtälön 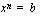 . Nuo luvut ovat toistensa vastalukuja ja niistä se positiivinen on luvun
. Nuo luvut ovat toistensa vastalukuja ja niistä se positiivinen on luvun 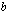
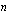 :s juuri
:s juuri 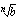 ja se negatiivinen ratkaisu tämän vastaluku
ja se negatiivinen ratkaisu tämän vastaluku 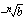 . Muistathan, että funktion arvon piti aina olla yksikäsitteinen. Kun sovitaan, että luvun parillinen juuri on aina ei-negatiivinen, saadaan myös parillinen juurifunktio määriteltyä yksikäsitteisesti: tällöin se negatiivinen luku, joka korotettuna juuren osoittamaan potenssiin
. Muistathan, että funktion arvon piti aina olla yksikäsitteinen. Kun sovitaan, että luvun parillinen juuri on aina ei-negatiivinen, saadaan myös parillinen juurifunktio määriteltyä yksikäsitteisesti: tällöin se negatiivinen luku, joka korotettuna juuren osoittamaan potenssiin 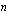 antaa myös juurrettavan, on tuon juurrettavan
antaa myös juurrettavan, on tuon juurrettavan 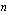 :nnen juuren vastaluku. Varmista vielä oheisella testaa tietosi -tehtävällä, että osaat määrittää jukujen yleisiä juuria.
:nnen juuren vastaluku. Varmista vielä oheisella testaa tietosi -tehtävällä, että osaat määrittää jukujen yleisiä juuria.
Testaa tietosi III
Huom! Osaathan määrittää yleisten juurien likiarvoja laskimella. Tämä hoituu näppäimellä, joka on laskimessasi todennäköisimmin joko
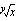 tai
tai 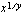 . Molemmat näppäimet toimivat samalla periaatteella eli ensin näpäillään juurrettava, sitten tuo juurinäppäin, tämän jälkeen annetaan juuren indeksi ja lopuksi näppäillään =. Esimerkiksi luvun
. Molemmat näppäimet toimivat samalla periaatteella eli ensin näpäillään juurrettava, sitten tuo juurinäppäin, tämän jälkeen annetaan juuren indeksi ja lopuksi näppäillään =. Esimerkiksi luvun 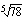 likiarvo saadaan laskimella seuraavien näppäilyjen kautta:
likiarvo saadaan laskimella seuraavien näppäilyjen kautta:
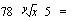 .
.
Tulos on viiden desimaalin tarkkuudella 2,39012.
Huom! Muistithan, että ne laskimen toiminnot, jotka on merkitty jonkun näppäimen yläpuolelle, toimivat INV- tai SHIFT-näppäimen kautta eli kyseisen toimintonäppäimen painallusta vastaa INV- tai SHIFT-näppäimen painallus ensin ja sitten merkinnän alla olevan näppäimen painallus.
Lue sitten esimerkit 4.10 ja 4.11, joista ilmenne pari tilannetta, joissa yleisten juurien määrittämistä tarvitaan. Luettuasi kyseiset esimerkit sinun pitäisi tietää, kuinka jonkun suureen määrä saadaan kätevästi laskettua esimerkiksi viiden aikajakson kuluttua, kun tiedetään suureen määrä alkuhetkellä ja että tuo määrä kasvaa tai vähenee aina yhtä monta prosenttia jokaisen aikajakson aikana. Harjoittele lopuksi asiaa oheisen oppimistehtävän avulla.
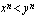 . Voidaanko tästä päätellä, että
. Voidaanko tästä päätellä, että 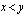 , kun
, kun 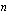 on parillinen? (ii)
on parillinen? (ii) 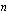 on pariton?
on pariton?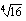 (b)
(b) 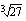 (c)
(c) 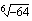 (d)
(d) 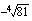 (e)
(e) 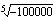
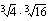 (b)
(b) 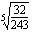 (c)
(c) 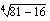
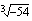
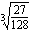
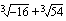
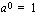
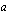 nollas potenssi
nollas potenssi 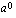 on aina yksi.
on aina yksi.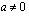
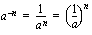
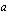 saadaan korotettua negatiiviseen potenssiin
saadaan korotettua negatiiviseen potenssiin 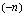 korottamalla luvun käänteisluku
korottamalla luvun käänteisluku 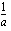 (osoittaja ja nimittäjä vaihtaneet paikkaa) vastaavaan positiiviseen potenssiin
(osoittaja ja nimittäjä vaihtaneet paikkaa) vastaavaan positiiviseen potenssiin 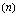 .
. 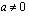
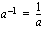
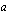 käänteisluku
käänteisluku 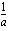 on sama kuin luku
on sama kuin luku 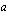 korotettuna potenssiin -1.
korotettuna potenssiin -1. 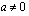
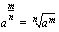
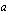 korotetaan murtolukupotenssiin
korotetaan murtolukupotenssiin 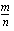 laskemalla eksponentin nimittäjän
laskemalla eksponentin nimittäjän 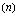 osoittama juuri eli
osoittama juuri eli 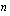 :s juuri luvusta
:s juuri luvusta 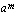 , missä
, missä 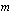 on eksponentin osoittaja.
on eksponentin osoittaja. 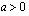
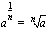
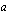
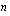 :s juuri on sama kuin luku
:s juuri on sama kuin luku 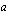 korotettuna potenssiin
korotettuna potenssiin 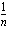 .
.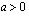
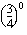 (b)
(b) 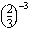 (c)
(c) 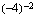 (d)
(d) 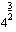 (e)
(e) 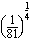 (f)
(f) 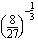
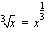 jne. Tätä taitoa kirjoittaa esim. juuret potensseina tarvitsemme seuraavissa moduleissa. Testaa oheisella testaa tietosi -tehtävällä, sujuuko sinulta erilaisten lausekkeiden muuntaminen potensseiksi.
jne. Tätä taitoa kirjoittaa esim. juuret potensseina tarvitsemme seuraavissa moduleissa. Testaa oheisella testaa tietosi -tehtävällä, sujuuko sinulta erilaisten lausekkeiden muuntaminen potensseiksi. 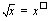 (b)
(b) 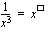 (c)
(c) 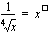
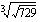 (b)
(b) 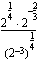 (c)
(c) 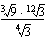
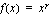 ,
,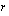 voi olla mikä tahansa reaaliluku. Tämä yleinen potenssifunktio on määritelty ainoastaan positiivisilla luvuilla.
voi olla mikä tahansa reaaliluku. Tämä yleinen potenssifunktio on määritelty ainoastaan positiivisilla luvuilla. 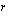 . Seuraavan oppimistehtävän avulla voit tutkia tätä kuvaajaa eri tapauksissa.
. Seuraavan oppimistehtävän avulla voit tutkia tätä kuvaajaa eri tapauksissa. 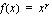 . Voit antaa eksponentille
. Voit antaa eksponentille 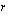 arvoja liikuttelemalla pistettä
arvoja liikuttelemalla pistettä 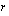 lukusuoralla. Ohjelma piirtää viereen potenssifunktion kuvaajan kyseisellä eksponentin arvolla. Tutki potenssifunktion käyttäytymistä ja vastaa sitten seuraaviin kysymyksiin.
lukusuoralla. Ohjelma piirtää viereen potenssifunktion kuvaajan kyseisellä eksponentin arvolla. Tutki potenssifunktion käyttäytymistä ja vastaa sitten seuraaviin kysymyksiin. 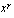 on aidosti kasvava?
on aidosti kasvava?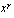 on vakio? Minka arvon funktio tuolloin saa kaikilla muuttujan arvoilla?
on vakio? Minka arvon funktio tuolloin saa kaikilla muuttujan arvoilla? 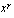 on aidosti vähenevä? Miksi?
on aidosti vähenevä? Miksi? 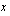 (
(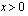 ) yhtälöstä
) yhtälöstä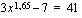 .
.