[edellinen] [sisällys] [seuraava]
2.6. Murtoyhtälö ja -epäyhtälö
Aloitetaan jälleen tarkastelemalla ensin vastaavaa funktiota eli tässä tapauksessa rationaalifunktiota.
2.6.1. Rationaalifunktio
Rationaalifunktio voidaan aina esittää muodossa
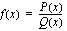 ,
,
missä 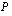 ja
ja 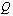 ovat polynomeja. Koska nollalla jakaminen on mahdotonta, on rationaalifunktio määritelty ainoastaan silloin, kun nimittäjä
ovat polynomeja. Koska nollalla jakaminen on mahdotonta, on rationaalifunktio määritelty ainoastaan silloin, kun nimittäjä 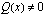 . Tarkastellaan ensin esimerkkinä erästä rationaalifunktiota.
. Tarkastellaan ensin esimerkkinä erästä rationaalifunktiota.
Esimerkki 2.24.
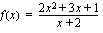 .
.
Rationaalifunktion kuvaajalla on aina vähintään yksi ns. asymptootti. Asymptootti on suora tai käyrä, jota funktion kuvaaja jatkuvasti lähestyy, mutta ei koskaan saavuta. Rationaalifunktion kuvaajaa voi hahmottaa myös sen asymptoottien avulla. Nämä löydetään seuraavasti:
- Rationaalifunktion kuvajalla on pystysuora asymptootti
 jokaisessa nimittäjän nollakohdassa
jokaisessa nimittäjän nollakohdassa 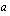 . Edellisessä esimerkissä esiintyneen funktion nimittäjän nollakohta on
. Edellisessä esimerkissä esiintyneen funktion nimittäjän nollakohta on 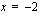 . Tämän funktion kuvaajalla on siten pystysuora asymptootti
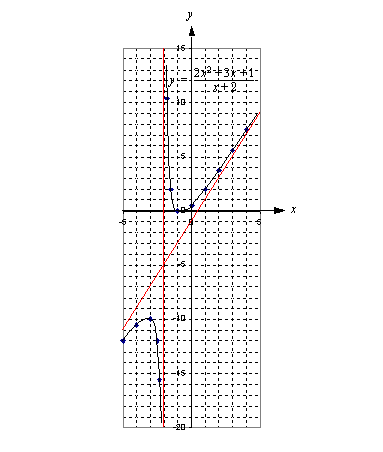
. Tämän funktion kuvaajalla on siten pystysuora asymptootti 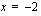 , joka on piirretty oheiseen kuvioon.
, joka on piirretty oheiseen kuvioon. - Lisäksi jokaisen rationaalifunktion kuvaajalla on asymptootti, joka kuvaa funktion kulkua äärettömyydessä. (Äärettömän symboli on
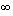 .) Tämä asymptootti löydetään suorittamalla rationaalifunktion jakolasku esimerkiksi jakokulmassa. Tehdään tämä edelliselle esimerkkifunktiollemme.
.) Tämä asymptootti löydetään suorittamalla rationaalifunktion jakolasku esimerkiksi jakokulmassa. Tehdään tämä edelliselle esimerkkifunktiollemme. 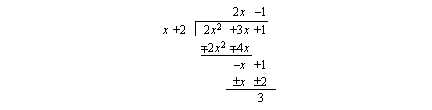
Jako ei nyt mennyt tasan. Tämä merkitsee vain sitä, että
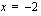 ei ole osoittajapolynomin nollakohta. Kun jakolasku ei mene tasan, vaan jää jakokäännös, ilmoitamme jakolaskun tuloksen seuraavasti:
ei ole osoittajapolynomin nollakohta. Kun jakolasku ei mene tasan, vaan jää jakokäännös, ilmoitamme jakolaskun tuloksen seuraavasti: eli jakolaskun tulokseen lisätään ns. jäännöstermi, joka on jakojäännös jaettuna jakajalla (kuten tavallisten lukujenkin tapauksessa). Voimme nyt esittää funktiomme myös tässä uudessa muodossa:
Tästä muodosta on helppo päätellä, mitä funktion arvoille tapahtuu, kun muuttujan
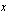 arvot kasvavat tai vähenevät rajatta eli kun ne lähestyvät ääretöntä tai miinus ääretöntä. Jos
arvot kasvavat tai vähenevät rajatta eli kun ne lähestyvät ääretöntä tai miinus ääretöntä. Jos 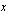 vähenee tai kasvaa rajatta, tekee samoin myös jäännöstermin nimittäjä
vähenee tai kasvaa rajatta, tekee samoin myös jäännöstermin nimittäjä 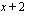 . Kun osoittaja on koko ajan 3 ja nimittäjä on itseisarvoltaan hyvin suuri, lähestyy osamäärä nollaa ts. mitä suuremmalla luvulla jaamme lukua 3, sitä pienempi on osamäärä. Jäännöstermi lähestyy siis nollaa, kun muuttuja
. Kun osoittaja on koko ajan 3 ja nimittäjä on itseisarvoltaan hyvin suuri, lähestyy osamäärä nollaa ts. mitä suuremmalla luvulla jaamme lukua 3, sitä pienempi on osamäärä. Jäännöstermi lähestyy siis nollaa, kun muuttuja 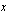 kasvaa tai vähenee rajatta. Tätä merkitään:
kasvaa tai vähenee rajatta. Tätä merkitään:Koska jäännöstermi lähestyy nollaa hyvin suurilla ja hyvin pienillä muuttujan arvoilla, lähestyvät esimerkkifunktiomme arvot muuttujan arvojen kasvaessa tai vähentyessä rajatta funktion
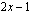 arvoja:
arvoja: Esimerkkifunktiomme kulkua äärettömyydessä kuvaa siten suora
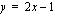 , joka on funktion kuvaajan toinen asymptootti. Se on myös piirretty oheiseen kuvioon.
, joka on funktion kuvaajan toinen asymptootti. Se on myös piirretty oheiseen kuvioon. Suorittamalla rationaalifunktion osoittaman jakolaskun esimerkiksi jakokulmassa ja esittämällä funktion uudella tavalla saadun osamäärän ja jäännöstermin avulla voi aina päätellä, mitä funktion arvoille tapahtuu muuttujan arvojen kasvaessa tai vähentyessä rajatta. Se funktio, jonka arvoja tarkasteltavan rationaalifunktion arvot lähestyvät hyvin suurilla ja hyvin pienillä muuttujan arvoilla, kertoo tämän rationaalifunktion kuvaajan asymptootin.
2.6.2. Murtoyhtälö
Murtoyhtälö voidaan sieventää muotoon
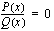 ,
,
missä 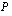 ja
ja 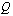 ovat polynomeja. Murtoyhtälöitä käsiteltäessä on aina muistettava, että rationaalifunktio ei ole määritelty nimittäjän nollakohdissa. On hyvä huomioida murtoyhtälön määrittelyjoukko heti aluksi ennen kuin tekee yhtälölle muita toimenpiteitä. Kun lopulta on saanut yhtälön kaikki juuriehdokkaat, on niistä hylättävä määrittelyjoukkoon kuulumattomat luvut eli nimittäjän nollakohdat.
ovat polynomeja. Murtoyhtälöitä käsiteltäessä on aina muistettava, että rationaalifunktio ei ole määritelty nimittäjän nollakohdissa. On hyvä huomioida murtoyhtälön määrittelyjoukko heti aluksi ennen kuin tekee yhtälölle muita toimenpiteitä. Kun lopulta on saanut yhtälön kaikki juuriehdokkaat, on niistä hylättävä määrittelyjoukkoon kuulumattomat luvut eli nimittäjän nollakohdat.
Luentomonisteessa murtoyhtälön ratkaisemista on esitelty esimerkein luvussa 2.5.1. Ota tuo luku esille ja katso esimerkkiä 2.18. Siinä on ratkaistu sama yhtälö kahdella eri tavalla. Huomaa, että ennen muita toimenpiteitä on mietitty, mitä arvoja muuttuja ei ainakaan voi saada eli on rajattu nimittäjän nollakohdat pois ratkaisuvaihtoehdoista. Aina, kun ratkaistavana oleva yhtälö tai epäyhtälö ei ole määritelty kaikilla luvuilla, on syytä miettiä, mitkä arvot ovat sallittuja, jotta niitä ei virheellisesti hyväksy ratkaisuiksi. Kun määrittelyjoukon miettii heti aluksi, se ei niin helposti unohdu ratkaisutoimenpiteitä suorittaessa.
Voit aina ratkaista murtoyhtälön kahdella eri tavalla. Esimerkissä ensimmäisenä esitelty tapa on pyrkiä poistamaan yhtälöstä nimittäjät kertomalla murtoyhtälö puolittain sopivalla lausekeella. Tätä lauseketta, jolla yhtälön kertoo puolittain, kannattaa pohtia ennen kuin suin päin aloittaa ratkaisemisen. Nimittäjien tulo tietysti kelpaa aina tuohon tarkoitukseen. Kuitenkin mitä korkeampaa astetta olevalla tekijällä yhtälön kertoo puolittain sitä korkeampaa astetta olevan yhtälön saa ratkaistavakseen. Itse jaan ensin nimittäjät tekijöihin ja valitsen lausekkeeksi, jolla kerron yhtälön puolittain, nimittäjissä esiintyvien eri tekijöiden tulon. Kun murtoyhtälö on kerrottu puolittain valitulla lausekkeella ja nimittäjät on supistettu pois, jää ratkaistavaksi tavallinen polynomiyhtälö. Lopuksi on vielä muistettava poistaa saaduista ratkaisuvaihtoehdoista nimittäjän nollakohdat.
Toinen tapa ratkaista murtoyhtälö on siirtää sen kaikki termit yhtälön toiselle puolelle ja suorittaa siellä merkityt laskutoimitukset, kunnes yhtälö tulee perusmuotoon, jossa toisella puolella on yksi ainoa rationaalifunktio ja toisella puolella luku nolla:
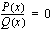 .
.
Koska tiedämme, että osamäärä on nolla ainoastaan silloin, kun osoittaja on nolla, toteutuu tämä yhtälö, kun osoittajapolynomi 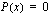 . Näin saadaan jälleen ratkaistavaksi tavallinen polynomiyhtälö.
. Näin saadaan jälleen ratkaistavaksi tavallinen polynomiyhtälö.
Luettuasi esimerkit luentomonisteesta voit harjoitella murtoyhtälön ratkaisemista oheisen oppimistehtävän avulla. Harjoittele molempia tapoja, jotta huomaat eron niiden periaatteeissa.
2.6.3. Murtoepäyhtälö
(epäyhtälössä voi tietysti olla mikä tahansa muu epäyhtälömerkki) ratkaiseminen perustuu osamäärän merkkisääntöön: osamäärä 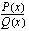 on
on
Murtoepäyhtälön ratkaiseminen muistuttaa paljon edellä opeteltua korkeamman asteen epäyhtälön ratkaisemista. Aluksi murtoepäyhtälö sievennetään muotoon, jossa epäyhtälön toisella puolella on vain luku nolla ja toisella puolella yksi rationaalilauseke. Näin tapahtuu, kun siirretään murtoepäyhtälön kaikki termit sen toiselle puolelle ja suoritetaan laskutoimitukset. Osamäärän merkkisääntöä sovelletaan, kun epäyhtälö on ensin perusmuodossaan
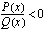 .
.
Tämän jälkeen selvitetään 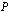 :n ja
:n ja 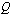 :n nollakohdat. Osamäärän merkin tutkimista varten laaditaan merkkikaavio samalla tavoin kuin korkeamman asteen epäyhtälön tapauksessa. Merkkikaaviosta ilmenee, millä väleillä osoittaja
:n nollakohdat. Osamäärän merkin tutkimista varten laaditaan merkkikaavio samalla tavoin kuin korkeamman asteen epäyhtälön tapauksessa. Merkkikaaviosta ilmenee, millä väleillä osoittaja 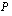 ja nimittäjä
ja nimittäjä 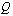 ovat positiiviset ja millä väleillä negatiiviset. Tämän jälkeen on merkkikaavion avulla helppo päätellä osamäärän merkkisääntöä hyödyntäen, millä väleillä näiden polynomien osamäärä on positiivinen ja millä väleillä negatiivinen.
ovat positiiviset ja millä väleillä negatiiviset. Tämän jälkeen on merkkikaavion avulla helppo päätellä osamäärän merkkisääntöä hyödyntäen, millä väleillä näiden polynomien osamäärä on positiivinen ja millä väleillä negatiivinen.
Edellä esitelty tapa on se, jota suosittelen murtoepäyhtälön ratkaisemiseksi. Erityisesti sinun on huomattava, että yleensä nimittäjiä ei kannata poistaa murtoepäyhtälöä ratkaistaessa. Jos esimerkiksi nimittäjät poistuisivat kertomalla epäyhtälö puolittain lausekkeella 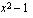 , ei tätä kannata tehdä, sillä lauseke voi saada sekä positiivisia että negatiivisia arvoja. Silloin, kun epäyhtälö kerrotaan puolittain negatiivisella luvulla, epäyhtälömerkin suunta vaihtuu. Em. tapauksessa epäyhtälön ratkaiseminen pitäisi jakaa osiin sen mukaan, saako lauseke, jolla epäyhtälö kerrotaan puolittain, positiivisia vai negatiivisia arvoja. Tämä tekee ratkaisun monimutkaiseksi eikä ole suositeltavaa. Älä siis kerro epäyhtälöä puolittain muuttujia sisältävällä lausekkeella muuta kuin siinä tapauksessa, että kyseinen lauseke saa aina vain positiivisia arvoja (tai vaihtoehtoisesti aina vain negatiivisia arvoja). Esimerkiksi lausekkeella
, ei tätä kannata tehdä, sillä lauseke voi saada sekä positiivisia että negatiivisia arvoja. Silloin, kun epäyhtälö kerrotaan puolittain negatiivisella luvulla, epäyhtälömerkin suunta vaihtuu. Em. tapauksessa epäyhtälön ratkaiseminen pitäisi jakaa osiin sen mukaan, saako lauseke, jolla epäyhtälö kerrotaan puolittain, positiivisia vai negatiivisia arvoja. Tämä tekee ratkaisun monimutkaiseksi eikä ole suositeltavaa. Älä siis kerro epäyhtälöä puolittain muuttujia sisältävällä lausekkeella muuta kuin siinä tapauksessa, että kyseinen lauseke saa aina vain positiivisia arvoja (tai vaihtoehtoisesti aina vain negatiivisia arvoja). Esimerkiksi lausekkeella 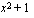 kertominen ei missään tilanteessa muuta epäyhtälömerkin suuntaa, koska se on aina positiivinen.
kertominen ei missään tilanteessa muuta epäyhtälömerkin suuntaa, koska se on aina positiivinen.
Muista myös huomioida murtoepäyhtälön määrittelyehto eli poistaa nimittäjien nollakohdat ratkaisujoukosta. Itse huomioin määrittelyehdon merkkikaaviota laatiessani. Selvitän aina heti aluksi nimittäjän nollakohdat, jotka eivät kelpaa ratkaisuiksi. Kun piirrän merkkikaavioon pystyviivat vastaamaan kutakin osoittajan ja nimittäjän nollakohtaa, piirrän samalla lukusuoralle nimittäjän nollakohtien kohdalle pienet avoimet pallukat sen merkiksi, että kyseiset luvut eivät kuulu määrittelyjoukkoon. Merkittyäni kaavioon ensin osoittajan ja nimittäjän merkit eri väleillä ja pääteltyäni osamäärän merkin eri väleillä ja katsoessani, millä väleillä epäyhtälön ehto toteutuu, huomaan näistä avoimista pallukoista, että ne eivät voi kuulua ratkaisujoukkoon.
Lue nyt luentomonisteesta luku 2.5.2 ja katso esimerkki 2.20, josta näet, kuinka murtoepäyhtälö muutetaan perusmuotoon ja kuinka ratkaisu päätellään merkkikaavion avulla. Huomaa, että yhtäsuuruuden ollessa mukana epäyhtälössä, tulevat osoittajan nollakohdat mukaan ratkaisujoukkoon. Kun merkkikaaviossa on nimittäjän nollakohta merkitty tuollaisella pienellä avoimella pallukalla, huomaa määrittelyjoukkoon kuulumatoman luvun sulkea pois ratkaisujoukosta. Tämän jälkeen voit vielä harjoitella murtoepäyhtälön ratkaisemista oheisella oppimistehtävällä.
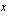 :n arvoilla funktio on määritelty?
:n arvoilla funktio on määritelty?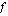 on määritelty, kun sen nimittäjä
on määritelty, kun sen nimittäjä 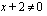 eli
eli 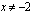 .
. 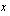
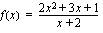

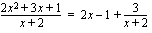
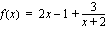 .
.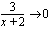 , kun
, kun 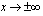 .
. 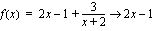 , kun
, kun 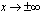 .
. 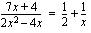 .
. 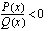
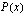 ja
ja 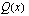 ovat samanmerkkiset ja
ovat samanmerkkiset ja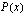 ja
ja 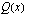 ovat erimerkkiset.
ovat erimerkkiset.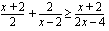 .
.