[edellinen] [sisällys] [seuraava]
2.4. Toisen asteen yhtälö ja epäyhtälö
Aloitetaan taas tarkastelemalla ensin vastaavaa funktiota.
2.4.1. Toisen asteen polynomifunktio
Toisen asteen polynomifunktio on muotoa
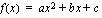 , missä
, missä 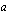 ,
, 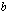 ja
ja 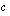 ovat vakioita ja
ovat vakioita ja 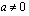 .
.
Tavallisesti funktion eri temien kertoimina olevat vakiot ovat reaalilukuja, sovellusesimerkeissä ne ovat joitakin mittayksiköllisiä vakioita. Toisen asteen termin kertoimen oletetaan olevan nollasta poikkeava, sillä jos se olisi nolla, funktio olisi ensimmäisen asteen polynomifunktio. Toisen asteen polynomifunktioita ovat esimerkiksi 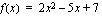 ja
ja 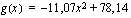 . Jälkimmäisessä esimerkkifunktiossa ensimmäisen asteen termin kerroin on nolla.
. Jälkimmäisessä esimerkkifunktiossa ensimmäisen asteen termin kerroin on nolla.
Toisen asteen polynomifunktion kuvaaja on paraabeli. Oheisen oppimistehtävän avulla voit tutkia, kuinka vakiot 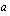 ,
, 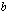 ja
ja 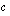 vaikuttavat paraabelin muotoon ja sijaintiin.
vaikuttavat paraabelin muotoon ja sijaintiin.
Oppimistehtävä 2.14.
Oheisesta osoitteesta löydät ohjelman, joka piirtää toisen asteen polynomifunktion kuvaajan vakioiden 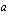 ,
, 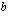 ja
ja 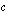 eri arvoilla. Voit liikutella näitä vakioita omilla lukusuorillaan ja samalla näet kyseisten vakioiden numeerisen arvon ja toisen asteen polynomifunktion kuvaajan näillä vakiokertoimien arvoilla. Tutki kokeilemalla vakioiden
eri arvoilla. Voit liikutella näitä vakioita omilla lukusuorillaan ja samalla näet kyseisten vakioiden numeerisen arvon ja toisen asteen polynomifunktion kuvaajan näillä vakiokertoimien arvoilla. Tutki kokeilemalla vakioiden 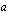 ,
, 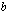 ja
ja 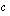 vaikutusta toisen asteen polynomifunktion kuvaajaparaabeliin ja vastaa seuraaviin kysymyksiin.
vaikutusta toisen asteen polynomifunktion kuvaajaparaabeliin ja vastaa seuraaviin kysymyksiin.
http://home.netvigator.com/~wingkei9/javagsp/ax2bxc.html
(a) Mitkä kertoimista 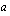 ,
, 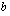 ja
ja 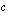 vaikuttavat paraabelin muotoon?
vaikuttavat paraabelin muotoon?
(b) Milloin paraabeli aukeaa ylöspäin ja milloin se aukeaa alaspäin?
(c) Mihin kertoimien 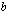 ja
ja 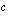 muuttaminen vaikuttaa
muuttaminen vaikuttaa
(i) paraabelin muotoon (ii) paraabelin sijaintiin?
(d) Miten kertoimen 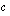 muuttaminen vaikuttaa paraabeliin? Mitä kerroin
muuttaminen vaikuttaa paraabeliin? Mitä kerroin 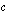 ilmoittaa paraabelista?
ilmoittaa paraabelista?
Huom!
Jos annat vakiolle 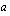 arvon nolla, voit tutkia em. linkistä löytyvällä ohjelmalla, kuinka ensimmäisen asteen kerroin ja vakiotermi vaikuttavat ensimmäisen asteen polynomifunktion kuvaajaan ts. suoraan.
arvon nolla, voit tutkia em. linkistä löytyvällä ohjelmalla, kuinka ensimmäisen asteen kerroin ja vakiotermi vaikuttavat ensimmäisen asteen polynomifunktion kuvaajaan ts. suoraan.
Opetellaan vielä piirtämään toisen asteen polynomifunktion kuvaaja, ennen kuin aloitetaan toisen asteen yhtälöiden tarkastelu. Toisen asteen polynomifunktion kuvaajan voi toki aina piirtää laskemalla siltä pisteitä ja piirtämällä kuvaajan koordinaatistoon näiden pisteiden avulla. Opetan nyt kuitenkin vielä toisen tavan, jossa ei tarvitse määrittää paraabelilta kuin sen huippupiste, muut löytyvät päättelemällä.
Tiedämme, että paraabelin 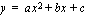 kerroin
kerroin 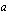 yksinään määrää sen muodon. Erityisesti kerroin
yksinään määrää sen muodon. Erityisesti kerroin 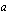 määrää paraabelin aukeamissuunnan:
määrää paraabelin aukeamissuunnan: 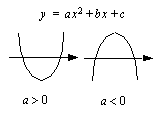
Paraabelin piirtäminen onnistuu mukavasti näiden tietojen avulla seuraavalla tavalla:
-
Määrätään ensin paraabelin
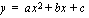 huippu. Huipun
huippu. Huipun 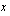 -koordinaatti on
-koordinaatti on
ja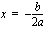 ,
,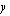 -koordinaatti voidaan laskea tämän avulla sijoittamalla paraabelin yhtälöön. [Se, että huipun
-koordinaatti voidaan laskea tämän avulla sijoittamalla paraabelin yhtälöön. [Se, että huipun 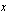 -koordinaatti on
-koordinaatti on 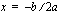 voidaan päätellä seuraavasti: huipussa on derivaatan nollakohta eli
voidaan päätellä seuraavasti: huipussa on derivaatan nollakohta eli 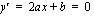 , josta saadaan ratkaistua
, josta saadaan ratkaistua 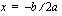 . Koska derivaatta tulee vasta myöhemmin tällä kurssilla, annetaan tämä tieto tässä vaiheessa valmiina.]
. Koska derivaatta tulee vasta myöhemmin tällä kurssilla, annetaan tämä tieto tässä vaiheessa valmiina.]
-
Tämän jälkeen ajatellaan tuo huippupiste origoksi ja piirretään siihen muotoa
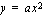 oleva paraabeli. Tuon paraabelin muita pisteitä löydetään seuraavasti: Annetaan ensin
oleva paraabeli. Tuon paraabelin muita pisteitä löydetään seuraavasti: Annetaan ensin 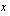 :lle arvo 1 ja lasketaan
:lle arvo 1 ja lasketaan 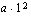 , mikä on
, mikä on 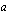 . Pisteet löytyvät koordinaatistosta menemällä huippupisteestä yhden yksikön verran sekä oikealle että vasemmalle (paraabeli symmetrinen akselinsa suhteen) ja
. Pisteet löytyvät koordinaatistosta menemällä huippupisteestä yhden yksikön verran sekä oikealle että vasemmalle (paraabeli symmetrinen akselinsa suhteen) ja 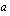 :n verran ylös- tai alaspäin
:n verran ylös- tai alaspäin 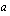 :n etumerkistä riippuen. Annetaan sitten
:n etumerkistä riippuen. Annetaan sitten 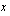 :lle arvo 2 ja lasketaan
:lle arvo 2 ja lasketaan 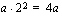 . Nyt paraabelin uudet pisteet löytyvät menemällä huippupisteestä kaksi askelta oikealle ja vasemmalle ja
. Nyt paraabelin uudet pisteet löytyvät menemällä huippupisteestä kaksi askelta oikealle ja vasemmalle ja 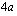 :n verran ylös- tai alaspäin sen mukaan, aukeaako paraabeli ylös- vai alaspäin. Näin jatketaan antamalla vuorostaan
:n verran ylös- tai alaspäin sen mukaan, aukeaako paraabeli ylös- vai alaspäin. Näin jatketaan antamalla vuorostaan 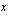 :lle arvo 3 ja laskemalla
:lle arvo 3 ja laskemalla 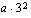 , joka näyttää, minkä verran liikutaan
, joka näyttää, minkä verran liikutaan 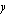 -akselin suunnassa, kun mennään huippupisteestä kolme askelta oikealle ja vasemmalle.
-akselin suunnassa, kun mennään huippupisteestä kolme askelta oikealle ja vasemmalle.
Seuraava esimerkki demonstroikoon tarkemmin paraabelin piirtämistä tällä periaatteella.
-
Tämän jälkeen ajatellaan tuo huippupiste origoksi ja piirretään siihen muotoa
Esimerkki 2.15.
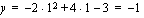 .
.
Paraabelin huippupiste on 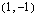 . Paraabelia piirrettäessä tämä piste ajatellaan origoksi. Lasketaan sitten huippupisteestä laskettuja eri suuria
. Paraabelia piirrettäessä tämä piste ajatellaan origoksi. Lasketaan sitten huippupisteestä laskettuja eri suuria 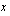 -akselin suuntaisia siirtymiä vastaavat
-akselin suuntaisia siirtymiä vastaavat 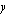 -akselin suuntaiset siirtymät. Esitän ne nyt selvyyden vuoksi taulukkona. Normaalisti nämä päätellään päässä laskien.
-akselin suuntaiset siirtymät. Esitän ne nyt selvyyden vuoksi taulukkona. Normaalisti nämä päätellään päässä laskien.
Piirretään nyt tiedetyt paraabelin pisteet koordinaatistoon ja hahmotellaan paraabeli kulkemaan näiden pisteiden kautta.
Huom!
Tämä menettely on hyvä tapa paraabelin piirtämiseksi, kunhan on huolellisesti laskenut huippupisteen. Jos huippu on väärin, menevät muutkin pisteet väärin. Tästä syystä paraabelin piirrettyään kannattaa tarkistaa sen yhtälön avulla yksi tai kaksi pistettä saamaltaan kuvaajalta. Nyt esimerkiksi tiedämme paraabelin yhtälöstä, että se kulkee pisteen 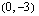 kautta.
kautta.
2.4.2. Toisen asteen yhtälö
Lue, mitä luentomonisteessa sanotaan toisen asteen yhtälöstä ja sen ratkaisemisesta luvussa 2.3.1. Esimerkki 2.10 liittyy fysiikkaan, sen voit huoletta sivuuttaa. Oleellisinta on, että luettuasi tiedät, että toisen asteen yhtälön
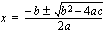 .
.
Tätä kaavaa tulet tarvitsemaan jatkuvasti tällä kurssilla, joten se sinun kannattaa opetella ulkoa.
Tällä kaavalla voit ratkaista minkä tahansa toisen asteen yhtälön. Kuitenkin silloin, kun yhtälö on ns. vaillinainen toisen asteen yhtälö eli siitä puuttuu joko ensimmäisen asteen termi tai vakiotermi, saat ratkaistua yhtälön helposti muutenkin. Vakiotermin puuttuessa voit ottaa polynomista 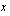 :n yhteiseksi tekijäksi ja ratkaista yhtälön tulon nollasäännöllä: kahden tai useamman tekijän tulo on nolla, jos ja vain jos jokin sen tekijöistä on nolla. Esimerkiksi näin:
:n yhteiseksi tekijäksi ja ratkaista yhtälön tulon nollasäännöllä: kahden tai useamman tekijän tulo on nolla, jos ja vain jos jokin sen tekijöistä on nolla. Esimerkiksi näin:
Jos taas toisen asteen yhtälöstä puuttuu ensimmäisen asteen termi, se ratkeaa helposti seuraavalla tavalla:
Sinun on myös hyvä tietää, kuinka toisen asteen yhtälön ratkaisujen lukumäärän voi selvittää diskriminantin avulla. Diskriminantiksi kutsutaan toisen asteen yhtälön ratkaisukaavassa esiintyvän juurilausekkeen juurrettavaa ts. yhtälön 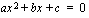 diskriminantti
diskriminantti 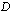 on
on
2.4.3. Toisen asteen epäyhtälö
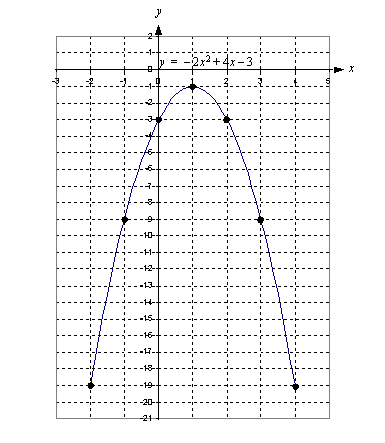
Lue ensin, mitä luentomonisteessa sanotaan toisen asteen epäyhtälöistä ja niiden ratkaisemisesta luvussa 2.3.2. On tärkeää, että luettuasi tekstin ymmärrät, että toisen asteen epäyhtälön ratkaisu päätellään vastaavan polynomifunktion kuvaajan perusteella. Tuota kuvaajaa ei tietenkään tarvitse tarkasti piirtää - riittää, että tietää, missä kohdissa kuvaaja leikkaa 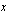 -akselin (jos leikkaa) ja mikä on paraabelin aukeamissuunta. Alkuvaiheessa kannattaa aina piirtää karkea kuva tästä tilanteesta samalla tavoin kuin monisteen esimerkeissä oli tehty. Kun olet ratkaissut useita toisen asteen epäyhtälöitä, sinulle riittää, että hahmotat funktion kuvaajaparaabelin kulun mielessäsi. Aina kuitenkin toisen asteen epäyhtälön ratkaisu päätellään vastaavan funktion kuvaajan perusteella. Nyt on sinun vuorosi harjoitella tätä ratkaisemista.
-akselin (jos leikkaa) ja mikä on paraabelin aukeamissuunta. Alkuvaiheessa kannattaa aina piirtää karkea kuva tästä tilanteesta samalla tavoin kuin monisteen esimerkeissä oli tehty. Kun olet ratkaissut useita toisen asteen epäyhtälöitä, sinulle riittää, että hahmotat funktion kuvaajaparaabelin kulun mielessäsi. Aina kuitenkin toisen asteen epäyhtälön ratkaisu päätellään vastaavan funktion kuvaajan perusteella. Nyt on sinun vuorosi harjoitella tätä ratkaisemista.
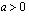 , paraabeli aukeaa ylöspäin ja
, paraabeli aukeaa ylöspäin ja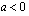 , paraabeli aukeaa alaspäin.
, paraabeli aukeaa alaspäin. 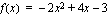 kuvaaja.
kuvaaja. 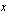 -koordinaatti on
-koordinaatti on 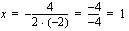 .
.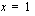 saadaan huipun
saadaan huipun 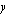 -koordinaatiksi
-koordinaatiksi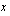 -akselin suuntainen siirtymä
-akselin suuntainen siirtymä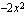
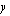 -akselin suuntainen siirtymä
-akselin suuntainen siirtymä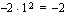
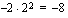
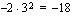
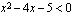 .
. 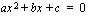
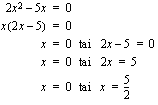
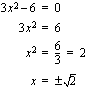
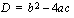 .
.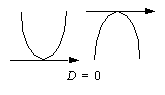
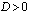 , yhtälöllä
, yhtälöllä 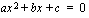 on kaksi eri ratkaisua,
on kaksi eri ratkaisua,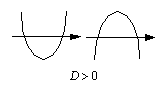
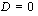 , yhtälöllä on yksi ratkaisu, joka on ,
, yhtälöllä on yksi ratkaisu, joka on ,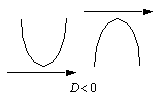
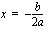 .
. 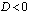 , yhtälöllä ei ole lainkaan reaaliratkaisua.
, yhtälöllä ei ole lainkaan reaaliratkaisua. 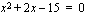 (b)
(b) 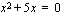 (c)
(c) 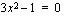
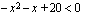 (b)
(b)