[edellinen] [sisällys] [seuraava]
1.6. Prosenttilaskuja
Prosenttilaskut ovat talousmatematiikan perusta ja yksi niistä matematiikan osa-alueista, joiden hallitseminen on hyödyllistä kenelle tahansa. Esitestin mukaan myös teille juuri prosenttilaskut olivat yleisimpiä arkielämässä tarvittavasta matematiikasta. Kurssimonisteessa on lyhyt esittely esimerkkeineen prosenttiosuuden, prosenttimuutoksen ja kasvuasteen laskemisesta. Lue se ensin ja harjoittele sitten niiden määrittämistä oheisten oppimis- ja testaa tietosi -tehtävien avulla. Jos asiat ovat kovin tuttuja, voit toki siirtyä suoraan harjoituksiin.
Oppimistehtävä 1.8.
Herra Lahtinen osti Jyväskylän keskustasta yksiön sijoitusasunnoksi. Hän maksoi asunnosta 52200 euroa. Lahtinen vuokraa asunnon opiskelijalle hintaan 335 euroa/kk. Vuokratuloista hän maksaa yhtiövastiketta 70 euroa/kk. Jäljelle jäävästä summasta Lahtiselta peritään vielä pääomaveroa 29 %. Kuinka monta prosenttia Lahtinen saa vuodessa korkotuloja sijoittamastaan pääomasta?
Sinusta saattaa tuntua monisteen esimerkkejä ja näiden oppimistehtävien malliratkaisuja lukiessasi, että laskisit itse hieman toisin. Se on aivan luonnollista: jokainen meistä ajattelee omalla tavallaan. Laske vain omalla tavallasi; malliratkaisun avulla voit yleensä päätellä, oliko tapasi oikein. Yritä löytää se laskutapa, joka parhaiten sopii omaan ajatteluusi. Muista, että oikeaan ratkaisuun on lukuisia eri reittejä. Itse käytän näissä esimerkeissä prosenttilukujen desimaalimuotoa, sillä olen kokenut sen helpoimmaksi laskiessani tulosten likiarvoja taskulaskimella.
Tiedäthän eron prosentin ja prosenttiyksikön välillä? Puhekielessä ja jopa tiedotusvälineissä kuulee käytettävän näitä käsitteitä väärin. Opi olemaan tarkkana oman kielenkäyttösi suhteen: kahden prosentin ja kahden prosenttiyksikön suuruinen muutos on aivan eri asia.
Ohessa on ote Nordea-pankin Joustoluoton sopimusehdoista:
"Luotonsaaja joutuu maksamaan saamastaan luotosta vuotuista korkoa 6 ________ (=marginaali) yli 3 kk:n euriborkoron (=viitekorko)."
Kumpi sana tyhjässä kohdassa pitäisi lukea:
(a) prosenttia (b) prosenttiyksikköä?
Oppimistehtävä 1.9.
Laurin palkka on 1720 euroa/kk. Siitä menee veroa 21,5 %, eläke- ja työttömyysvakuutusmaksua 4,8 % ja ammattiyhdistyksen jäsenmaksua 1,3 %. Hän suunnittelee työpaikan vaihtoa. Uudessa paikassa palkka olisi 5 % nykyistä suurempi, mutta samalla vero kasvaisi 1,0 prosenttiyksikköä. Kuinka monta prosenttia ja mihin suuntaan muuttuisi Laurin nettopalkka työpaikan vaihdoksen jälkeen?
Kaikissa tilanteissa ei tarvitse tietää perusarvoa, vaan prosenttimuutos voidaan määrittää pelkkien prosenttilukujen avulla. Tällöin laskuissa merkitään perusarvoa jollakin yleisellä tunnuksella, kuten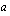 
, 
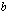tai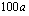 
, 
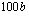jne. Muuttuneet arvot lasketaan tämän avulla ja prosenttimuutos määritetään vertaamalla uutta arvoa alkuperäiseen perusarvoon. Kurssimonisteen esimerkistä 1.21 näit, miten tällaisissa tilanteissa toimitaan. Kokeile tällaista harjoitusta vielä seuraavan oppimistehtävän avulla.
Oppimistehtävä 1.10.
Uuden työehtosopimuksen takia yrityksen on nostettava kuukausipalkkojaan 3,2 %. Samalla se vähentää henkilökuntaansa 5 %. Kuinka monta prosenttia ja mihin suuntaan muuttuvat työvoimakustannukset?
Aina silloin, kun on tärkeää kertoa, missä ajassa tietty prosenttimuutos tapahtuu, se ilmoitetaan kasvuasteena eli prosentteina jossakin aikayksikössä. Muun muassa erilaisten sijoitusten tuotot ja tilien korkokannat ilmoitetaan kasvuasteina eli niistä ilmenee, missä ajassa kyseinen tuotto sijoitetulle pääomalle saadaan. Esimerkiksi edellä olleessa oppimistehtävässä 1.8 oli itse asiassa laskettavana herra Lahtisen sijoitusasunnon tuoton kasvuaste prosentteina vuodessa.
Voit vielä harjoitella kasvuasteen laskemista oheisen oppimistehtävän avulla.