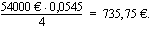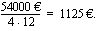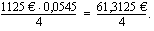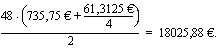[edellinen] [sisällys] [seuraava]
1.2. Aritmeettinen jono ja summa
1.2.1. Aritmeettinen jono
Lukujono on aritmeettinen, jos sen minkä tahansa kahden peräkkäisen jäsenen erotus on vakio eli
Testaa tietosi I
Muodostetaan aritmeettinen lukujono, kun sen ensimmäinen jäsen on 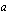 ja kahden peräkkäisen jäsenen erotus
ja kahden peräkkäisen jäsenen erotus 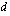 . Näiden tietojen perusteella voidaan muodostaa koko lukujono.
. Näiden tietojen perusteella voidaan muodostaa koko lukujono.
Esimerkki 1.3.
Esimerkki 1.4.
Pariskunta ottaa 42000 euron asuntolainan 12 vuodeksi. Lainan korkokanta on 5,25 %/vuosi. Laina maksetaan takaisin puolivuosittain tapahtuvin tasalyhennyksin. Samalla maksetaan korko jäljellä olevasta lainasta. Kuinka suuri on kahdeskymmenes maksuerä?
Selvitetään vielä maksettava korko. Ensimmäisessä erässä korkoa maksetaan 42000 eurosta, toisessa erässä 40250 eurosta, kolmannessa 38500 eurosta jne. Pääomat, joille korko lasketaan, muodostavat vähenevän aritmeettisen lukujonon. Samoin tekevät korot, jotka ovat
Kahden peräkkäisen erän koron erotus on aina 45,9375 euroa, mikä on 5,25 %:n vuotuisen korkokannan mukainen korko 1750 euron lyhennyksestä puolelta vuodelta laskettuna.
Koska maksuerien korot muodostavat aritmeettisien jonon, jonka 1. jäsen on 1102,50 euroa ja kahden peräkkäisen jäsenen erotus -45,9375 euroa, on kahdennenkymmenennen maksuerän korko
1.2.2. Aritmeettinen summa
Aritmeettisella summalla tarkoitetaan aritmeettisen jonon 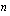 ensimmäisen jäsenen summaa, jota merkitään tunnuksella
ensimmäisen jäsenen summaa, jota merkitään tunnuksella 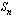 . Edellä käytettyjä merkintöjä käyttäen aritmeettinen summa on
. Edellä käytettyjä merkintöjä käyttäen aritmeettinen summa on
Johdetaan yksinkertainen kaava aritmeettisen summan laskemiseksi. Kirjoitetaan summa ensin alusta loppuun ja sitten päinvastaisessa järjestyksessä. Merkitään jonon viimeistä jäsentä tunnuksella 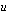 . Toiseksi viimeinen jäsen on silloin
. Toiseksi viimeinen jäsen on silloin 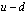 , kolmanneksi viimeinen
, kolmanneksi viimeinen 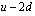 jne.
jne.
Jos aritmeettisen summan termien lukumärä on 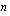 , ensimmäinen yhteenlaskettava
, ensimmäinen yhteenlaskettava 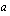 ja viimeinen yhteenlaskettava
ja viimeinen yhteenlaskettava 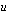 , niin aritmeettinen summa on
, niin aritmeettinen summa on
Koska 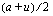 on aritmeettisen summan ensimmäisen ja viimeisen yhteenlaskettavan keskiarvo, voidaan aritmeettisen summan kaava tulkita niin, että siinä kerrotaan ensimmäisen ja viimeisen yhteenlaskettavan keskiarvo termien lukumärällä.
on aritmeettisen summan ensimmäisen ja viimeisen yhteenlaskettavan keskiarvo, voidaan aritmeettisen summan kaava tulkita niin, että siinä kerrotaan ensimmäisen ja viimeisen yhteenlaskettavan keskiarvo termien lukumärällä.
Esimerkki 1.6.
Esimerkki 1.7.
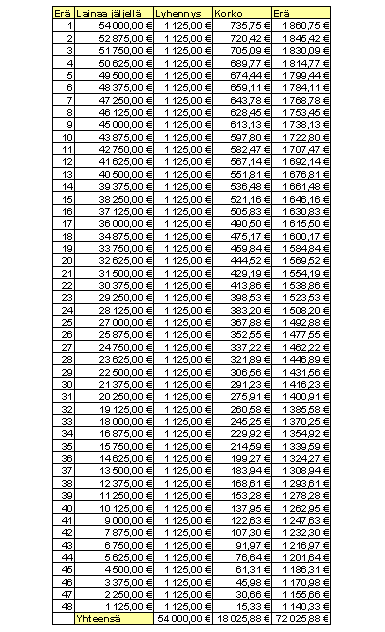
Pariskunta on ottanut 54000 euron asuntolainan 12 vuodeksi. Lainan korkokanta on 5,45 %/vuosi. Laina maksetaan takaisin neljännesvuosittain tapahtuvin tasalyhennyksin. Samalla maksetaan korko jäljellä olevasta lainasta. Kuinka paljon lainasta joudutaan kaikkiaan maksamaan korkoa?
Aiemmin esitetyn esimerkin perusteella tiedetään, että tasalyhennyslainan maksuerien korot muodostavat vähenevän aritmeettisen jonon. Ensimmäinen korko maksetaan koko lainasta ja se on
Oppimistehtävä 1.8.
Laske, kuinka paljon oppimistehtävän 1.5 lainasta on kaikkiaan maksettava korkoa.
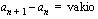 kaikilla
kaikilla 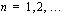
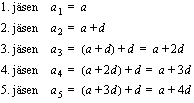
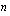 . jäsen on
. jäsen on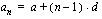 .
.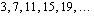
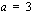 ja kahden peräkkäisen termin erotus
ja kahden peräkkäisen termin erotus 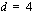 , on sen kahdestoista jäsen
, on sen kahdestoista jäsen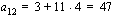 .
.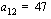
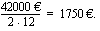
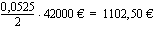
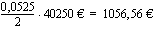
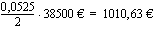
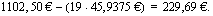
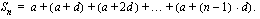
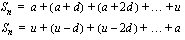
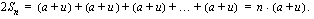
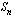 :
: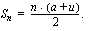
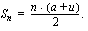
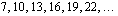
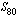 .
. 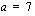 ja kahden peräkkäisen jäsenen erotus
ja kahden peräkkäisen jäsenen erotus 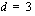 . Tällöin jonon kahdeksaskymmenes jäsen on
. Tällöin jonon kahdeksaskymmenes jäsen on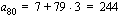 .
.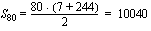 .
.