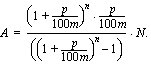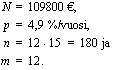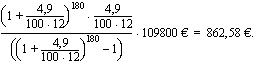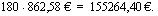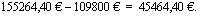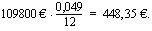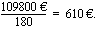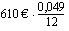[edellinen] [sisällys] [seuraava]
2.3. Tasaerälaina
Tasaerälainaa maksetaan kunakin eräpäivänä takaisin vakiosumma. Tämä tasaerä sisältää koron jäljellä olevasta lainasta ja loppu erästä on lainan lyhennystä. Lainapääoman vähenemisen myötä koron osuus tasaerässä pienenee ja lyhennyksen osuus kasvaa. Tässä osiossa opetellaan laskemaan tasaerälainan tasaerä sekä laatimaan lainanlyhennystaulukko, josta ilmenee kunakin eräpäivänä maksetun tasaerän sisältämä korko ja lyhennys. Lisäksi vertaillaan tasaerä- ja tasalyhennyslainojen kokonaiskorkojen määriä.
Tasaerälainan takaisinmaksun vakiosumma eli tasaerä määräytyy niin, että lainaohjelman mukaan maksettujen tasaerien yhteinen alkuarvo lainanottohetkellä sovitun korkokannan mukaan on lainan suuruinen. Nyt, kun osaamme määrittää jaksollisten suoritusten yhteisen alkuarvon, osaamme myös laskea tasaerän suuruuden. Aloitetaan tarkastelu yksinkertaisimmasta tapauksesta.
2.3.1. Annuiteettilaina
Tarkastellaan aluksi sellaisia tasaerälainoja, joissa erät maksetaan vuosittain. Näitä kutsutaan annuiteettilainoiksi. Johdetaan lauseke annuiteettilainan tasaerän eli annuiteetin laskemiseksi. Otetaan käyttöön seuraavat merkinnät:
Lainaohjelman mukaan ensimmäinen tasaerä 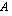 euroa maksetaan vuoden kuluttua lainanottohetkestä. Toinen tasaerä maksetaan kahden vuoden kuluttua jne. Kun laina-aika on
euroa maksetaan vuoden kuluttua lainanottohetkestä. Toinen tasaerä maksetaan kahden vuoden kuluttua jne. Kun laina-aika on 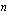 vuotta, viimeinen eli
vuotta, viimeinen eli 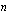 . tasa-erä maksetaan tämän ajan kuluttua. Lasketaan ensin näiden jaksollisten suoritusten yhteinen loppuarvo korkokannan
. tasa-erä maksetaan tämän ajan kuluttua. Lasketaan ensin näiden jaksollisten suoritusten yhteinen loppuarvo korkokannan 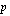 %/vuosi mukaan viimeisen tasaerän maksuhetkellä eli
%/vuosi mukaan viimeisen tasaerän maksuhetkellä eli 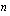 vuoden kuluttua lainanottohetkestä.
vuoden kuluttua lainanottohetkestä.
Määrätään ensin kunkin annuiteetin arvo (kasvanut pääoma) 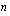 . annuiteetin maksuhetkellä
. annuiteetin maksuhetkellä 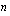 vuoden kuluttua lainanottohetkestä.
vuoden kuluttua lainanottohetkestä.
2. suoritus: 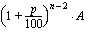 (kasvanut korkoa
(kasvanut korkoa 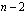 vuotta)
vuotta)
1. suoritus: 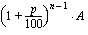 (kasvanut korkoa
(kasvanut korkoa 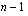 vuotta)
vuotta)
Tasaeristä muodostuneet kasvaneet pääomat muodostavat päättyvän 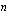 -jäsenisen geometrisen jonon, jonka ensimmäinen jäsen on
-jäsenisen geometrisen jonon, jonka ensimmäinen jäsen on 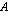 ja kahden peräkkäisen jäsenen suhdeluku
ja kahden peräkkäisen jäsenen suhdeluku 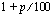 . Tästä syystä näiden jaksollisten suoritusten yhteinen loppuarvo on geometrinen summa, jossa
. Tästä syystä näiden jaksollisten suoritusten yhteinen loppuarvo on geometrinen summa, jossa
Tasaerien yhteinen loppuarvo on geometrisen summan kaavan avulla
Diskontataan tämä summa lainanottohetkeen. Alkuperäinen pääoma, joka korkokannan 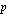 %/vuosi mukaan kasvaa
%/vuosi mukaan kasvaa 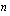 vuoden aikana tasaerien yhteisen loppuarvon suuruiseksi on
vuoden aikana tasaerien yhteisen loppuarvon suuruiseksi on
Tasaerä määrätyy siten, että tämä tasaerien yhteinen alkuarvo on lainan suuruinen. Muodostetaan yhtälö, jossa saatu tasaerien yhteinen alkuarvo merkitään yhtäsuureksi kuin laina 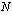 euroa:
euroa:
Ratkaistaan tästä yhtälöstä tasaerä 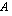 . Kerrotaan yhtälö ensin puolittain vasemman puolen nimittäjällä, jolloin saadaan
. Kerrotaan yhtälö ensin puolittain vasemman puolen nimittäjällä, jolloin saadaan
Jos annuiteettlilaina on 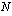 euroa, sen korkokanta
euroa, sen korkokanta 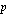 %/vuosi ja laina-aika
%/vuosi ja laina-aika 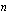 vuotta, niin lainasta vuosittain maksettava tasaerä eli annuiteetti
vuotta, niin lainasta vuosittain maksettava tasaerä eli annuiteetti 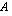 on
on
Esimerkki 2.13.
Perhe ottaa 75000 euron asuntolainan 15 vuodeksi. Lainan korkokanta on 5,4 %/vuosi. Laina korkoineen maksetaan takaisin vuosittain maksettavin tasaerin. Laske tämä vuosittainen tasaerä eli annuiteetti. Kuinka paljon lainasta joudutaan kaikkiaan maksamaan korkoa?
Annuiteettilainan tasaerän laskemiseksi on taulukkolaskentaohjelmissa yleensä oma funktio. Excel-taulukkolaskentaohjelmalla lainan tasaerän voi laskea funktiolla, joka englanninkielisessä versiossa on PMT(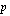 %;
%;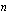 ;
;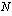 ;0;0) ja suomenkielisessä versiossa MAKSU(
;0;0) ja suomenkielisessä versiossa MAKSU(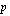 %;
%;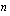 ;
; ;0;0). Funktion ensimmäinen argumentti on korkojakson korkokanta, joka ilmoittaa, mikä osuus pääomasta maksetaan korkoa yhden korkojakson aikana. Toinen argumentti ilmoittaa maksuerien lukumäärän, joka annuiteettilainassa on sama kuin laina-aika vuosina. Kolmas argumentti on jaksollisten maksujen alkuarvo eli lainamäärä. Neljäs argumentti on maksun ns. tuleva arvo, joksi asetetaan lainan tasaerää laskiessa aina 0. Viides argumentti on luku 0 tai 1 riippuen siitä tapahtuvatko maksut jakson lopussa (arvo 0) vai jakson alussa (arvo 1). Näin laskien funktiolla saadaan tulokseksi negatiivinen maksu, joka on itseisarvoltaan oikein. Halutessasi tasaerän taulukkoon positiivisena lisää PMT/MAKSU-funktion eteen - (miinus-merkki).
;0;0). Funktion ensimmäinen argumentti on korkojakson korkokanta, joka ilmoittaa, mikä osuus pääomasta maksetaan korkoa yhden korkojakson aikana. Toinen argumentti ilmoittaa maksuerien lukumäärän, joka annuiteettilainassa on sama kuin laina-aika vuosina. Kolmas argumentti on jaksollisten maksujen alkuarvo eli lainamäärä. Neljäs argumentti on maksun ns. tuleva arvo, joksi asetetaan lainan tasaerää laskiessa aina 0. Viides argumentti on luku 0 tai 1 riippuen siitä tapahtuvatko maksut jakson lopussa (arvo 0) vai jakson alussa (arvo 1). Näin laskien funktiolla saadaan tulokseksi negatiivinen maksu, joka on itseisarvoltaan oikein. Halutessasi tasaerän taulukkoon positiivisena lisää PMT/MAKSU-funktion eteen - (miinus-merkki).
Edellisen esimerkin annuiteetti voidaan laskea Excelin PMT-funktiolla antamalla seuraavat argumentit:
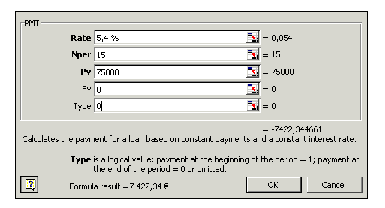
Kuviosta ilmenee, kuinka varsinaisen PMT-funktion tulos on negatiivinen. Taulukon solussa olevan kaavan tulos on kuitenkin lainan annuiteetti positiivisena, koska olen asettanut itse kaavan antamaan tämän PMT-funktion tuloksen vastaluvun. Annuiteetin laskevassa solussa on siis kaava:
=-PMT(5,4 %;15;75000;0;0).
Seuraavaksi harjoitellaan tasaerälainan lainanlyhennystaulukon laatimista. Tällöin seurataan, kuinka koron ja lyhennyksen osuus tasaerissä muuttuu. Jokainen erä sisältää koron jäljellä olevasta lainasta. Loppuosa tasaerästä on lyhennystä. Jos tasaerä on mukavuuden vuoksi pyöristetty, ei viimeinen erä aina ole muiden erien suuruinen, koska silloin maksetaan pois koko jäljellä oleva laina korkoineen.
Esimerkki 2.14.
Edellisen esimerkin annuitettilainan tasaerä pyöristetään yhden euron tarkkuuteen. Laadi lainanlyhennystaulukko, josta ilmenee kunkin erän sisältämä korko ja lyhennys. Kuinka suuri on viimeinen maksuerä, jolloin maksetaan takaisin jäljellä oleva laina ja sen korko? Laske myös maksettu kokonaiskorko.
Euron tarkkuuteen pyöristetty tasaerä on 7422 euroa. Alla on esitetty Excel-taulukkolaskentaohjelmalla laadittu lainanlyhennystaulukko.
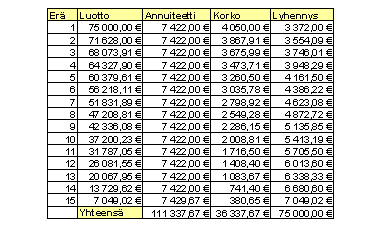
Luotto-sarakkeeseen on laskettu, kuinka paljon lainaa on jäljellä. Jäännöslaina saadaan vähentämällä edellisestä jäännöslainasta tasaerän sisältämä lyhennys. Annuiteetti-sarakkeessa on maksettu tasaerä. Korko-sarakkeessa on tasaerän sisältämä korko, joka saadaan laskemalla 5,4 % jäljellä olevasta lainasta, koska maksujakso on yksi vuosi eli kokonainen korkojakso. Lyhennys-sarakkeeseen on laskettu tasaerän sisältämä lyhennys vähentämällä korko maksetusta tasaerästä. Viimeinen maksuerä on saatu laskemalla yhteen jäljellä oleva laina ja sen korko yhdeltä vuodelta.
Oppimistehtävä 2.15.
Herra Lahtinen ottaa sijoittamista varten lainaa 25200 euroa 8 vuodeksi. Lainan korkokanta on 4,85 %/vuosi.
(a) Laadi lainanlyhennystaulukko ja laske kokonaiskorko, kun laina maksetaan takaisin vuosittain tapahtuvin yhtäsuurin lyhennyksin ja erien yhteydessä maksetaan myös korko jäljellä olevalle lainalle.
(b) Laske vuosittainen tasaerä (annuiteetti), jos laina maksetaankin takaisin yhtäsuurissa vuosittaisissa erissä. Laadi lainanlyhennystaulukko, josta ilmenee tasaerän sisältämä korko ja lyhennys, kun tasaerä pyöristetään euron tarkkudelle. Kuinka suuri on tällöin viimeinen maksuerä? Kuinka paljon kaikkiaan joudutaan maksamaan korkoa?
2.3.2. Tasaerälaina, jossa useita tasaeriä korkojakson aikana
Pankkilainan ottanut asiakas haluaa yleensä jakaa lainan maksurasituksen tasaisesti koko vuoden ajaksi. Tasaerälainojen maksuerät maksetaan usein puolivuosittain, neljännesvuosittain tai kuukausittain. Kun näissä tapauksissa lasketaan lainan tasaerää, lasketaan vuotuisen korkokannan avulla maksujaksolle korkokanta seuraavasti: puolen vuoden korkokanta on vuosittainen korkokanta jaettuna kahdella, neljännesvuoden korkokanta vuosittaisen korkokannan neljäsosa ja kuukausittainen korkokanta vuotuisen korkokannan kahdestoistaosa. Tasaerä lasketaan edellä johdetulla annuiteetin kaavalla, johon on vuotuisen korkokannan tilalle sijoitettu näin laskettu jakson korkokanta.
Excel-taulukkolaskentaohjelmalla tasaerän voi laskea helposti myös silloin, kun korkojakson aikana on useita tasaeriä. Tasaerä lasketaan tällöin samalla funktiolla kuin annuiteettilainan annuiteetti eli englanninkielisessä versiossa funktiolla PMT(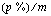 ;
;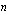 ;
;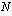 ;0;0) ja suomenkielisessä versiossa funktiolla MAKSU(
;0;0) ja suomenkielisessä versiossa funktiolla MAKSU(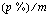 ;
;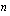 ;
;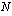 ;0;0). Funktion ensimmäinen argumentti on korkojakson korkokanta, joka ilmoittaa, mikä osuus pääomasta maksetaan korkoa yhden korkojakson aikana. Maksujakson korkokanta saadaan jakamalla vuotuinen korkokanta
;0;0). Funktion ensimmäinen argumentti on korkojakson korkokanta, joka ilmoittaa, mikä osuus pääomasta maksetaan korkoa yhden korkojakson aikana. Maksujakson korkokanta saadaan jakamalla vuotuinen korkokanta 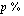 vuoden maksukertojen lukumäärällä
vuoden maksukertojen lukumäärällä 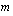 . Funktion muut argumentit ovat samat kuin annuiteettia laskettaessa. Muista laittaa tasaerän laskentakaavaan tämän funktion vastaluku halutessasi taulukkoosi maksettavan tasaerän positiivisena.
. Funktion muut argumentit ovat samat kuin annuiteettia laskettaessa. Muista laittaa tasaerän laskentakaavaan tämän funktion vastaluku halutessasi taulukkoosi maksettavan tasaerän positiivisena.
Esimerkki 2.16.
Perhe ottaa omakotitalon hankkimista varten asuntolainaa 109800 euroa 15 vuodeksi. Lainan korkokanta on 4,9 %/vuosi. Laina maksetaan takaisin kuukausittain tapahtuvin tasaerin. Laske tasaerä ja kokonaiskorko. Kuinka paljon korkoa olisi jouduttu kaikkiaan maksamaan, jos olisi valittu tasaerälainan sijasta kuukausittain maksettava tasalyhennyslaina?
Lasketaan vielä kokonaiskorko, jos kyseessä olisi tasalyhennyslaina. Tiedetään, että tasalyhennyslainan maksuerien korot muodostavat aritmeettisen lukujonon, joten korkojen yhteissumma voidaan laskea aritmeettisena summana, kun tiedetään erien lukumäärä sekä ensimmäisen ja viimeisen erän korko. Eriä on 180. Ensimmäinen korko maksetaan koko lainasta kuukauden ajalta, joten se on
Vastaavan tasalyhennyslainan kokonaiskorko on ensimmäisen ja viimeisen maksuerän korkojen keskiarvo kerrottuna erien lukumäärällä eli
Oppimistehtävä 2.17.
Jouni otti kolmeksi vuodeksi 6300 euron autolainan. Lainan korkokanta on 8,55 %/vuosi. Laina maksetaan takaisin neljännesvuosittain tapahtuvin tasaerin. Laske tasaerä sekä laadi lainanlyhennystaulukko, josta ilmenee erien sisältämä korko ja lyhennys. Kuinka paljon Jouni joutuu tasaerälainastaan kaikkiaan maksamaan korkoa? Kuinka paljon pienempi kokonaiskorko olisi, jos Jouni olisikin päätynyt neljännesvuosittain maksettavaan tasalyhennyslainaan?

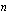 . suoritus :
. suoritus : 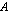
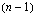 . suoritus:
. suoritus: 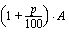 (kasvanut korkoa vuoden)
(kasvanut korkoa vuoden)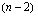 . suoritus:
. suoritus: 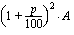 (kasvanut korkoa 2 vuotta)
(kasvanut korkoa 2 vuotta)
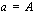 (1. yhteenlaskettava),
(1. yhteenlaskettava),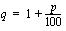 (suhdeluku) ja
(suhdeluku) ja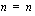 (termien lukumäärä).
(termien lukumäärä).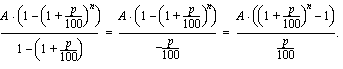
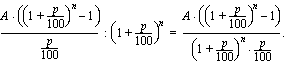
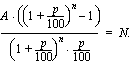
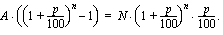
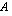 ratkeaa jakamalla yhtälö puolittain tämän tuntemattoman kertoimella, jolloin saadaan
ratkeaa jakamalla yhtälö puolittain tämän tuntemattoman kertoimella, jolloin saadaan 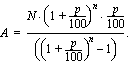
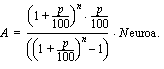
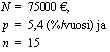
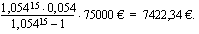
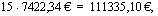

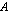 seuraavalla kaavalla:
seuraavalla kaavalla: