Ratkaisu tehtävään 6.5

a ) Yhtälö on määritelty, kun

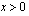
Suoraan logaritmin määritelmän nojalla.

b ) Yhtälö on määritelty, kun 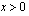ja 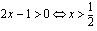. Molemmat määrittelyt ovat voimassa, kun .

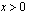Yhtälön molemmilla puolilla on samankantaiset logaritmit, joten logaritmin monotonisuuden nojalla.

.

c ) Yhtälö on määritelty, kun .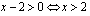

Suoraan logaritmin määritelmän nojalla.

d ) Yhtälö on määritelty .

Vähennetään ensin yhtälön molemmilta puolilta .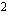

Logaritmin määritelmän nojalla.

Otetaan neliöjuuri puolittain. Huomioidaan mahdollinen negatiivinen ratkaisu.

e ) Yhtälö on määritelty, kun .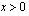

Muokataan yhtälöä logaritmin määritelmän avulla johdettujen laskusääntöjen avulla.

Vähennetään yhtälön molemmilta puolilta .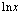

Logaritmin määritelmän nojalla.

[Tehtävä 6.5][Vinkki tehtävään 6.5]

[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]