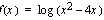 on määritelty, kun logaritmin lauseke, joka on toisen asteen polynomi
on määritelty, kun logaritmin lauseke, joka on toisen asteen polynomi 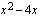 on suurempaa kuin nolla. Määrittelyjoukko saadaan, kun ratkaistaan epäyhtälö
on suurempaa kuin nolla. Määrittelyjoukko saadaan, kun ratkaistaan epäyhtälö 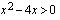 . Epäyhtälön ratkaisemiseksi on ratkaistava vastaava yhtälö
. Epäyhtälön ratkaisemiseksi on ratkaistava vastaava yhtälö 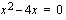 .
.
a ) Logaritmifunktio 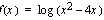 on määritelty, kun logaritmin lauseke, joka on toisen asteen polynomi
on määritelty, kun logaritmin lauseke, joka on toisen asteen polynomi 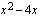 on suurempaa kuin nolla. Määrittelyjoukko saadaan, kun ratkaistaan epäyhtälö
on suurempaa kuin nolla. Määrittelyjoukko saadaan, kun ratkaistaan epäyhtälö 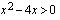 . Epäyhtälön ratkaisemiseksi on ratkaistava vastaava yhtälö
. Epäyhtälön ratkaisemiseksi on ratkaistava vastaava yhtälö 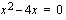 .
.
Yhtälö ratkaistaan ottamalla yhteiseksi tekijäksi 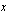 .
.
Tulon nollasäännön mukaan tulo on nolla, jos toinen tulon tekijöistä on nolla.
Epäyhtälö on tosi, kun  , sillä logaritmin sisäfunktion
, sillä logaritmin sisäfunktion 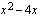 kuvaaja on ylöspäin aukeava paraabeli, joten
kuvaaja on ylöspäin aukeava paraabeli, joten 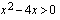 , kun
, kun  .
.
b ) Eksponenttifunktio 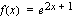 on määritelty
on määritelty 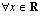 .
.
[Tehtävä 6.3][Vinkki tehtävään 6.3]