Ratkaisu tehtävään 3.3

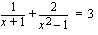
Ratkaistaan yhtälön määrittelyjoukko: Yhtälö ei ole määritelty rationaalilausekkeiden nimittäjien nollakohdiss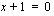a ja .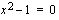

vähennetään molemmilta puolilta 1, jolloin yhtälöstä 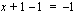saadaan ratkaistua .

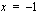Summan ja erotuksen avulla saadaan yhtälö muotoon 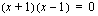ja tulon nollasäännön avulla joko 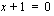tai 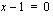. Edellinen on tarkasteltu jo edellä ja jälkimmäisestä saadaan lisäämällä molemmille puolille 1 ratkaistua 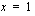. Yhtälö on siis määritelty, kun .

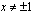Ratkaistaan yhtälö laventamalla ensin vasemman puolen murtolausekkeet samannimisiksi ja laskemalla ne yhteen.

Kerrotaan seuraavaksi molemmat puolet vasemman puolen nimittäjän lausekkeella 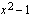, jolloin saadaan yhtälöä sieventämällä toisen asteen yhtälö, joka voidaan ratkaista toisen asteen yhtälön ratkaisukaavan avulla.

Yhtälön ratkaisu on siis .

Toisella tapaa voidaan päätyä ratkaisuun, kun muokataan yhtälöä hieman enemmän. Jaetaan nimittäjä tekijöihinsä, joka on jo edellä tehty ja supistetaan tekijällä .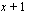

Nyt kertomalla molemmat puolet lausekkeella 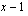ratkaistavaksi jää ensimmäisen asteen yhtälö.

Vältyttiin siis ensimmäisen tavan toisen asteen yhtälön ratkaisulta, joka ei kuulu määrittelyjoukkoon.

[Tehtävä 3.3][Vinkki tehtävään 3.3]

[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]