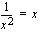Opiskelutehtäviä
OT 1.1.
Funktio on jatkuva ja aidosti monotoninen ja sen määrittelyjoukko 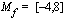 ja arvojoukko
ja arvojoukko 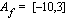 .
.
a ) Hahmottele erään ehdot toteuttavan funktion kuvaaja.
b ) Onko tällä funktiolla käänteisfunktiota? Jos on, määrää 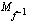 ja
ja 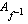 . Hahmottele lisäksi käänteisfunktion kuvaaja.
. Hahmottele lisäksi käänteisfunktion kuvaaja.
[Vinkki tehtävään 1.1]
OT 1.3.
Funktiolla 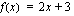 on käänteisfunktio.
on käänteisfunktio.
a ) Millä 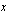 :n arvolla käänteisfunktio saa arvon 2?
:n arvolla käänteisfunktio saa arvon 2?
b ) Määritä 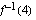 .
.
c ) Piirrä funktioiden 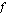 ja
ja 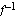 kuvaajat.
kuvaajat.
d ) Laske 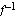 .
.
[Vinkki tehtävään 1.3]
OT 1.4.
Mitkä seuraavista väitteistä pitävät paikkansa?
a ) Jos funktio on bijektio, on se myös injektio.
b ) Kun 3. asteen polynomifunktiolla 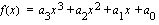 on kolme nollakohtaa, kirjoitetaan funktio tekijöidensä tulona
on kolme nollakohtaa, kirjoitetaan funktio tekijöidensä tulona 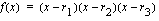 . Missä vakiot
. Missä vakiot 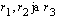 ovat funktion nollakohdat.
ovat funktion nollakohdat.
c ) Yhtälö on identtisesti tosi.
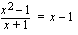
d ) Yhtälö on identtisesti tosi.
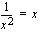
[Vinkki tehtävään 1.4]
OT 1.5.
Mitkä seuraavista väitteistä pitävät paikkansa funktiolle, joka on bijektio?
a ) Funktio on monotoninen
b ) Funktiolla on olemassa käänteisfunktio.
c ) Funktiolla on täsmälleen yksi nollakohta.
d ) Funktion määrittelyjoukossa ja arvojoukossa on täsmälleen yhtämonta alkiota.
[Vinkki tehtävään 1.5]
[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]
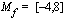 ja arvojoukko
ja arvojoukko 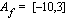 .
.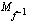 ja
ja 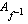 . Hahmottele lisäksi käänteisfunktion kuvaaja.
. Hahmottele lisäksi käänteisfunktion kuvaaja. 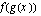 , kun
, kun 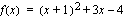 ja
ja 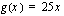 .
.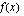 ja
ja 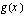 , jotka toteuttavat yhdistetyn funktion
, jotka toteuttavat yhdistetyn funktion 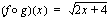
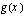 toteuttaa yhdistetyn funktion
toteuttaa yhdistetyn funktion 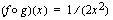 , kun ulkofunktio
, kun ulkofunktio 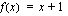 ?
?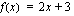 on käänteisfunktio.
on käänteisfunktio.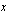 :n arvolla käänteisfunktio saa arvon 2?
:n arvolla käänteisfunktio saa arvon 2?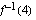 .
.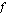 ja
ja 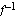 kuvaajat.
kuvaajat.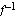 .
.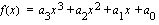 on kolme nollakohtaa, kirjoitetaan funktio tekijöidensä tulona
on kolme nollakohtaa, kirjoitetaan funktio tekijöidensä tulona 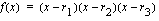 . Missä vakiot
. Missä vakiot 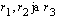 ovat funktion nollakohdat.
ovat funktion nollakohdat.