[edellinen] [sisällys] [seuraava]
7.3. Osittaisintegrointi ja integrointi sijoituksen avulla
Tähän mennessä opetetuilla integroimissäännöillä voidaan integroida vain pieni joukko funktioita. Ne eivät esimerkiksi sovellu yhdenkään yhdistetyn funktion integrointiin. Modulissa 4 opetettu yhdistetyn funktion derivoimissääntö voidaan kääntää integroimissäännöksi, mutta tällä kurssilla sivuutan tuon säännön. Opettelemme sen sijaan toisen integroimistavan, joka on em. sääntöä monikäyttöisempi eikä toisaalta teknisempänä menetelmänä vaadi niin paljon abstraktia ajattelua.
Opettelemme tässä luvussa myös toisen integroimistavan, joka soveltuu moniin ns. hankaliin integraaleihin eli sellaisten funktioiden integrointiin, joita ei aiemmin opetetuilla säännöillä voida integroida. Jälkimmäinen integrointitapa perustuu tulon derivoimiskaavaan. Se on kätevä monessa tilanteessa, mutta ei tietenkään sovi kaikkiin hankaliin integraaleihin. Näiden menetelmien opettelun jälkeenkin on helppo löyää funktioita, joita ei vielä osata integroida. Integrointi on paljon hankalampaa kuin derivointi, eikä aina ole helppoa tietää, mikä menetelmä tilanteeseen sopii. Tällä kurssilla annankin teille hankalammissa tapauksissa vihjeen, mitä menetelmää kannattaa tai voi käyttää. Kannattaa opetella nämä molemmat menetelmät hyvin, sillä joissakin tilanteissa vain toinen menetelmä toimii.
7.3.1. Integrointi sijoituksen avulla
Olen esitellyt integrointia sijoituksen avulla matematiikan peruskurssin monisteen luvussa 3.3.5. Tällä kertaa esitän asian kuitenkin toisin: esittelen tavan, jota voitte käyttää edellä sivuutettuun yhdistetyn funktion derivoimissääntöön perustuvaan integrointiin sekä useisiin muihin ns. hankaliin tapauksiin. Mikäli haluatte, voitte toki opiskella itsenäisesti asiat luentomonisteen tavoilla. Tässä esittämäni tapa on teknisempi menetelmä, jonka uskon olevan helpommin omaksuttavissa.
Integrointi sijoituksen avulla perustuu yhdistetyn funktion derivoimissääntöön. Sivuutan tässä kuitenkin menetelmän perustelut ja keskityn havainnollistamaan menetelmää esimerkkien avulla. Integroinnin tuloksenhan voi aina tarkastaa derivoimalla ja käytänkin tätä perusteluna esittämäni menetelmän oikeellisuudelle.
Integrointi sijoituksen avulla voidaan ajatella tekniikaksi, jossa hankalanoloinen integraali muutetaan yksinkertaisempaan muotoon vaihtamalla integroimismuuttuja. Tämä tapahtuu korvaamalla integroitavasta funktiosta jokin muuttujan 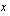 lauseke muuttujalla
lauseke muuttujalla 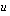 . (Luentomonisteen tavassa olen käyttänyt muuttujaa
. (Luentomonisteen tavassa olen käyttänyt muuttujaa 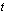 . Valitsin tähän tarkoituksella eri muuttujan, koska esitän nyt tavan hieman eri tavalla kuin luentomonisteessa.) Tällöin alkuperäinen integraali muuttuu yksinkertaisemmaksi integraaliksi tämän muttujan
. Valitsin tähän tarkoituksella eri muuttujan, koska esitän nyt tavan hieman eri tavalla kuin luentomonisteessa.) Tällöin alkuperäinen integraali muuttuu yksinkertaisemmaksi integraaliksi tämän muttujan 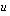 suhteen. Seuraavassa on esitelty menetelmän käyttö vaihe vaiheelta.
suhteen. Seuraavassa on esitelty menetelmän käyttö vaihe vaiheelta.
- Tavoitteena on yksinkertaistaa muuttujan
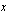 (voi tietysti olla jokin muukin muuttuja) suhteen hankala integraali helpommaksi muuttujan
(voi tietysti olla jokin muukin muuttuja) suhteen hankala integraali helpommaksi muuttujan 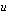 suhteen. Tätä varten valitaan integroitavasta funktiosta jokin muuttujan
suhteen. Tätä varten valitaan integroitavasta funktiosta jokin muuttujan 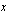 lauseke, jota merkitään uudella muuttujalla
lauseke, jota merkitään uudella muuttujalla 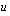 . Alkuvaiheessa voi olla vaikeaa tietää, mitä lauseketta muuttujalla
. Alkuvaiheessa voi olla vaikeaa tietää, mitä lauseketta muuttujalla 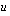 kannattaa merkitä. Yksi hyvä sääntö tähän on se, että jos integroitava funktio on yhdistetty funktio, kannattaa muuttujalla
kannattaa merkitä. Yksi hyvä sääntö tähän on se, että jos integroitava funktio on yhdistetty funktio, kannattaa muuttujalla 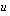 merkitä sen sisäfunktiota. Joissakin tapauksissa annan teille "sijoitusvihjeitä" siitä, mikä
merkitä sen sisäfunktiota. Joissakin tapauksissa annan teille "sijoitusvihjeitä" siitä, mikä 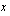 :n lauseke kannattaa korvata uudella muuttujalla
:n lauseke kannattaa korvata uudella muuttujalla 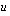 .
. - Tämän jälkeen integroitava funktio kirjoitetaan muuttujan
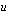 avulla sijoittamalla se valitun
avulla sijoittamalla se valitun 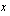 :n lausekkeen tilalle. Integraalimerkintään kuuluvan
:n lausekkeen tilalle. Integraalimerkintään kuuluvan 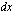 :n kirjoittamiseksi muuttujan
:n kirjoittamiseksi muuttujan 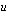 avulla lasketaan ensin
avulla lasketaan ensin 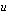 :lla korvatun muuttujan
:lla korvatun muuttujan 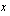 lausekkeen derivaatta muuttujan
lausekkeen derivaatta muuttujan 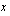 suhteen eli
suhteen eli 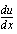 . (Muistathan, että derivaattaa
. (Muistathan, että derivaattaa 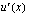 voidaan merkitä myös näin:
voidaan merkitä myös näin: 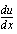 .) Tämän jälkeen ratkaistaan, mitä
.) Tämän jälkeen ratkaistaan, mitä 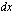 on
on 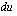 :n avulla lausuttuna tulkiten edellä käytetty derivaatan merkintä osamääräksi. Lopuksi tulos sijoitetaan
:n avulla lausuttuna tulkiten edellä käytetty derivaatan merkintä osamääräksi. Lopuksi tulos sijoitetaan 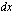 :n paikalle. Huomaa, että koko integroitava funktio on saatava näillä toimenpiteillä lausutuksi uuden muuttujan
:n paikalle. Huomaa, että koko integroitava funktio on saatava näillä toimenpiteillä lausutuksi uuden muuttujan 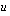 avulla. Myöhemmin esitettävät esimerkit valaiskoot paremmin tätä menetelmää.
avulla. Myöhemmin esitettävät esimerkit valaiskoot paremmin tätä menetelmää. - Tämän jälkeen ratkaistaan saatu integraali muuttujan
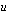 suhteen ja lopuksi palataan muuttujaan
suhteen ja lopuksi palataan muuttujaan 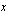 sijoitamalla integroinnin tuloksena saatuun
sijoitamalla integroinnin tuloksena saatuun 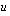 :n funktioon takaisin
:n funktioon takaisin 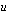 :n paikalle sen muuttujan
:n paikalle sen muuttujan 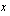 lauseke, joka aluksi korvattiin tällä uudella muuttujalla.
lauseke, joka aluksi korvattiin tällä uudella muuttujalla. Esimerkki 3.5.
Tarkista saamasi tulos derivoimalla.
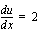 , josta
, josta 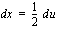 .
.
Sijoitetaan nämä integroitavaan funktioon, integroidaan muttujan 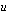 suhteen ja palataan lopulta takaisin muttujaan
suhteen ja palataan lopulta takaisin muttujaan 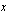 sijoittamalla saatuun tulokseen
sijoittamalla saatuun tulokseen 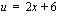 .
.
(b) Nyt integroitavana on yhdistetty funktio, jonka sisäfunktio on 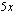 . Kokeillaan siis sijoitusta
. Kokeillaan siis sijoitusta 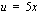 . Tällöin
. Tällöin
Edellisen esimerkin integraalit olisi voinut määrittää myös yhdistetyn funktion derivaatasta johdetulla integroimiskaavalla. Tällä tavoin vältyimme miettimästä, mikä on integroitavan sisä- tai ulkofunktio, mikä on sen sisäfunktion derivaatta, mikä on ulkofunktion integraalifunktio jne. Tällaista miettimistä tarvitaan kyseisen kaavan käytössä. Tässä käyttämämme menetelmä edellyttää vain, että tiedämme, mikä muuttujan 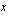 lauseke kannattaa korvata apumuuttujalla
lauseke kannattaa korvata apumuuttujalla 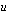 .
.
Esimerkki 3.6.
Tarkista saamasi tulos derivoimalla.
(a) Koska integroitavassa funktiossa esiintyy yhdistetty funktio, jonka sisäfunktio on 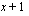 , kokeillaan sijoitusta
, kokeillaan sijoitusta 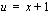 , jolloin
, jolloin
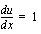 eli
eli 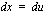 .
.
Kun 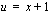 , on integroitavassa esiintyvä
, on integroitavassa esiintyvä 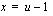 . Kirjoitetaan integroitava funktio uuden apumuuttujan avulla, integroidaan muuttujan
. Kirjoitetaan integroitava funktio uuden apumuuttujan avulla, integroidaan muuttujan 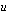 suhteen ja palataan lopuksi alkuperäiseen muuttujaan sijoittamalla saatuun tulokseen
suhteen ja palataan lopuksi alkuperäiseen muuttujaan sijoittamalla saatuun tulokseen 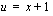 .
.
(b) Kokeillaan nyt yksinkertaistaa laskettavana oleva integraali sijoituksella 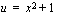 . (Mikäli tämä olisi harjoitustehtävä, antaisin sijoitusvihjeen.) Tällöin
. (Mikäli tämä olisi harjoitustehtävä, antaisin sijoitusvihjeen.) Tällöin
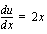 , josta
, josta 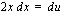 .
.
Integroitavassa funktiossa esiintyy 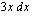 . Se, mitä tämän paikalle on sijoitettava, saadaan kertomalla edellä saatu yhtälö puolittain luvulla
. Se, mitä tämän paikalle on sijoitettava, saadaan kertomalla edellä saatu yhtälö puolittain luvulla 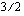 :
:
Oppimistehtävä 3.7.
ja tarkista saamasi tulos derivoimalla.
Integrointia sijoituksen avulla voidaan käyttää myös määrätyn integraalin laskemiseen. Tämä voidaan tehdä kahdella eri tavalla. Funktio voidaan ensin integroida edellä esitetyllä tavalla ja laskea sitten määrätty integraali tämän tuloksen avulla niin kuin aiemminkin. Seuraava esimerkki havainnollistakoon asiaa.
Esimerkki 3.8.
Toinen tapa määrätyn integraalin laskemiseksi sijoituksen avulla on vaihtaa muttujanvaihdon yhteydessä myös integroimisrajat, jolloin takaisinpaluuta alkuperäiseen muuttujaan ei tarvita. Kun alkuperäinen alaraja on 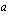 , on muuttujanvaihdossa asetettava uudeksi alarajaksi
, on muuttujanvaihdossa asetettava uudeksi alarajaksi 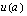 , missä
, missä 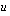 on sijoituksessa käytetty
on sijoituksessa käytetty 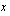 :n (tai muun alkuperäisen muuttujan) funktio. Vastaavasti vanhan ylärajan
:n (tai muun alkuperäisen muuttujan) funktio. Vastaavasti vanhan ylärajan 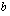 tilalle asetetaan muuttujanvaihdossa
tilalle asetetaan muuttujanvaihdossa 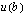 . Lasketaan vielä edellä esitetty esimerkki tällä uudella tavalla, jotta saatte kuvan menetelmän toiminnasta ja voitte samalla vertailla näitä määrätyn integraalin ratkaisutapoja.
. Lasketaan vielä edellä esitetty esimerkki tällä uudella tavalla, jotta saatte kuvan menetelmän toiminnasta ja voitte samalla vertailla näitä määrätyn integraalin ratkaisutapoja.
7.3.2. Osittaisintegrointi
Osittaisintegrointi on myös käyttökelpoinen monien hankalampien integraalien laskemiseen. Se perustuu tulon derivoimiskaavaan. Opiskele tämä integrointimenetelmä matematiikan peruskurssin luentomonisteen luvusta 3.3.4 sivulta 114 alkaen. Esimerkin 3.20 luettuasi voit itse harjoitella osittaisintegrointia oheisella oppimistehtävällä.
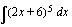 (b)
(b) 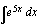
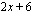 , sijoitetaan
, sijoitetaan 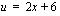 . Tällöin
. Tällöin 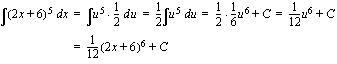
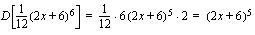
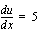 , josta
, josta 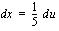 .
. 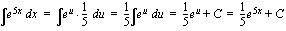
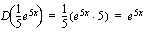
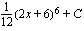 (b)
(b) 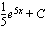
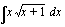 (b)
(b) 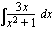
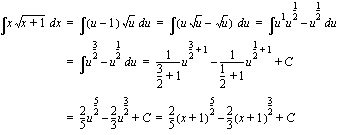
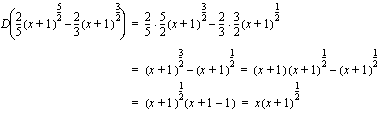
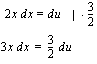
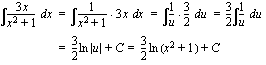
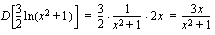
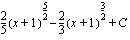 (b)
(b) 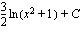
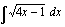
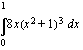 .
. 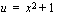 , jolloin
, jolloin 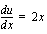 , josta
, josta 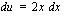 ja
ja 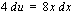 .
. 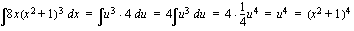
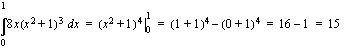
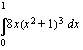 .
. 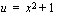 , jolloin uusi alaraja on
, jolloin uusi alaraja on 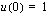 ja uusi yläraja
ja uusi yläraja 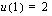 .
. 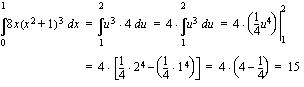
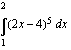 .
. 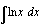 ,
, 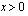 .
.