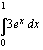[edellinen] [sisällys] [seuraava]
7.2. Määrätty integraali
Määrätty integraali on toinen integraalilaskennan peruskäsite. Määrätyn integraalin avulla voidaan mm. laskea, mikä on suureen tietyllä aikavälillä kertynyt määrä, kun sen kasvunopeus tunnetaan.
7.2.1. Määrätyn integraalin käsite
Lue ensin matematiikan propedeuttisen kurssin luentomonisteesta esimerkki 6.15 sivulta 173 alkaen. Tämä esimerkki johdattelee sinut määrätyn integraalin käsitteeseen. Lue sitten luvusta 6.3.1 määrätyn integraalin määritelmä sekä sen tulkinta käyrän ja koordinaattiakselin välisenä pinta-alana.
Kuinka funktion määrätty integraali sitten voidaan laskea? Määrätyn integraalin laskeminen sen määritelmään nojautuen on hankalaa ja työlästä ja vaatii yleensä tehokkaan laskulaitteen käyttämistä. Funktion määrätty integraali voidaan laskea sen integraalifunktion avulla. Se, kuinka tämä tapahtuu, on selvitetty analyysin peruslausetta käsittelevässä luvussa 6.3.2. Lue tästä luvusta kyseinen lause sekä sivulla 177 olevasta huomautuksesta alkaen, kuinka määrätyn integraalin arvo lasketaan analyysin peruslauseen nojalla, ja tutki tarkoin kaikki tätä laskutapaa valaisevat esimerkit 6.16 - 6.19. Monisteessa on myös esitetty perustelu analyysin peruslauseelle, mutta tämän osion voit hyvin sivuuttaa. Tällä kurssilla riittää, että opit laskemaan määrätyn integraalin arvon ja tunnet tärkeimmät määrätyn integraalin sovellukset, joita tarkastelemme hieman myöhemmin opittuamme ensin määrätyn integraalin määrittämiseen liittyvän laskutekniikan.
Tässä vielä yhteenveto määrätystä integraalista, jotta näkisitte, mikä on olennaisinta tietää tästä uudesta käsitteestä.
Määrätyn integraalin määritelmä
Olkoon funktio 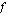 jatkuva suljetulla välillä
jatkuva suljetulla välillä 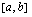 . Jaetaan väli
. Jaetaan väli 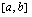
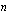 osaväliin vasemmanpuoleisen kuvan osoittamalla tavalla. Merkitään jakopisteitä tunnuksin
osaväliin vasemmanpuoleisen kuvan osoittamalla tavalla. Merkitään jakopisteitä tunnuksin 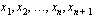 , missä
, missä 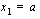 ja
ja 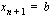 . Osavälien pituudet olkoot
. Osavälien pituudet olkoot 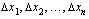 , missä
, missä 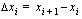 kaikilla
kaikilla 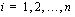 . Muodostetaan summa
. Muodostetaan summa
Kun jakopisteiden lukumäärä 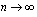 ja jakovälin pituus
ja jakovälin pituus 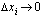 kaikilla
kaikilla 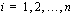 (ks. oikeanpuoleinen kuva), summa
(ks. oikeanpuoleinen kuva), summa 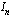 lähestyy raja-arvoa, joka on funktion
lähestyy raja-arvoa, joka on funktion 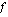 määrätty integraali
määrätty integraali 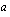 :sta
:sta 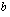 :hen ja jota merkitään
:hen ja jota merkitään
jos tämä raja-arvo on olemassa. Lukuja 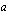 ja
ja 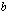 kutsutaan integroimisrajoiksi:
kutsutaan integroimisrajoiksi: 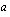 on alaraja ja
on alaraja ja 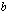 on yläraja.
on yläraja.
Määrätyn integraalin tulkintoja
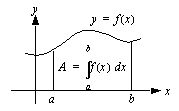 Geometrisesti tulkittuna funktion
Geometrisesti tulkittuna funktion 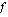 määrätty integraali
määrätty integraali 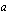 :sta
:sta 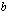 :hen on itseisarvoltaan funktion
:hen on itseisarvoltaan funktion 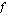 kuvaajan,
kuvaajan, 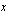 -akselin sekä suorien
-akselin sekä suorien 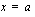 ja
ja 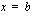 rajoittaman alueen pinta-ala.
rajoittaman alueen pinta-ala.
Funktion 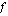 esittäessä jonkun suureen kasvunopeutta määrätty integraali
esittäessä jonkun suureen kasvunopeutta määrätty integraali
on tämän suureen välillä 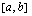 kertynyt määrä.
kertynyt määrä.
arvon laskeminen analyysin peruslauseen nojalla on kaksivaiheinen:
Vaiheessa, jossa funktio 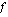 on integroitu, mutta integraalifunktion
on integroitu, mutta integraalifunktion 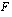 arvoja
arvoja 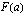 ja
ja 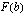 ei ole vielä laskettu käytetään merkintää
ei ole vielä laskettu käytetään merkintää
Huomaa, että määrätyn integraalin arvo on reaaliluku, kun taas integraalifunktio on jokin funktio.
http://www.cc.jyu.fi/~anvihola/testit/integraali/integraali.php
löydät havainnollistuksen määrätyn integraalin käsitteestä.
Harjoittele tämän jälkeen määrätyn integraalin laskemista oheisen oppimistehtävän avulla.
Oppimistehtävä 3.3.
Määrätyn integraalin ominaisuuksia
Määrätyn integraalin ominaisuuksia on lueteltu matematiikan peruskurssin luentomonisteen sivulla 111. Käy nuo ominaisuudet läpi ja huomaa erityisesti, että myös määrätyn integraalin tapauksessa voidaan summalle laskea määrätty integraali laskemalla se erikseen kullekin summan termille. Lisäksi integroitavan funktion vakiokerroin voidaan siirtää määrätyn integraalin kertoimeksi aivan samoin kuin integraalifunktiota määrättäessä.
7.2.2. Määrätyn integraalin sovelluksia
Tässä esitellään vain joitakin tavallisimpia määrätyn integraalin sovelluksia. Koska molemmat kurssilla käytössä olevat luentomonisteet kertovat näistä, on tässä vain yhteenveto siitä, mitä kannattaa opiskella mistäkin monisteesta.
Koska määrätty integraali voidaan tulkita käyrän ja koordinaattiakselin väliseksi pinta-alaksi, voidaan sitä käyttää tämäntyyppisten pinta-alojen määrittämiseen. Asiaa on esitelty tarkemmin matematiikan propedeuttisen kurssin luentomonisteen luvussa 6.3.5 sivulta 182 alkaen. Lue tästä, kuinka määrätyn integraalin avulla voidaan määrittää käyrän ja koordinaattiakselin rajoittama alue sekä kahden käyrän rajoittama alue. Käy myös läpi aiheisiin liittyvät esimerkit. Mikäli haluat harjoitella käyrien välisen pinta-alan laskemista, tee matematiikan peruskurssin luentomonisteesta oppimistehtävä 3.18 sivulta 114.
Funktion keskiarvo tietyllä välillä määritellään myös määrätyn integraalin avulla. Tämä on esitelty matematiikan peruskurssin luentomonisteen sivulla 114. Voit halutessasi harjoitella funktion keskiarvon määrittämistä oheisen oppimistehtävän avulla.
Oppimistehtävä 3.4.
Määrää funktion 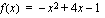 keskiarvo välillä
keskiarvo välillä 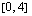 .
.
Kuten jo aiemmin määrätyn integraalin tulkintoja esitellessä tuli mainittua, määrätyn integraalin avulla voidaan laskea suureen tietyllä välillä kertynyt määrä, kun suureen kasvunopeus tunnetaan. Asiaa on esitelty tarkemmin matematiikan peruskurssin luentomonisteessa sivulla 112. Lue kyseinen kohta ja halutessasi voit lopuksi harjoitella suureen kertyneen määrän määrittämistä laskemalla kohdasta aiheeseen liittyvän oppimistehtävän 3.17.
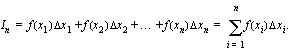
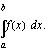
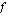 määrätty integraali
määrätty integraali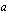 :sta
:sta 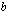 :hen on raja-arvo
:hen on raja-arvo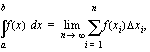
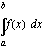
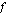 on jatkuva välillä
on jatkuva välillä 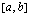 , niin määrätty integraali
, niin määrätty integraali 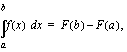
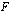 on jokin funktion
on jokin funktion 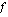 integraalifunktio.
integraalifunktio. 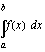
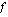 integraalifunktio
integraalifunktio 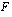 ja
ja 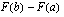 .
.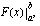
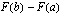 . Merkintä luetaan: "sijoitus
. Merkintä luetaan: "sijoitus 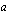 :sta
:sta 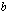 :hen funktiolle
:hen funktiolle 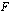 ". Siis
". Siis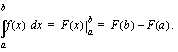
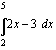 (b)
(b) 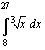 (c)
(c)