[edellinen] [sisällys] [seuraava]
5.2. Determinantti
Tässä luvussa opetellaan määrittämään neliömatriisin determinantti, joka on neliömatriisiin liittyvä reaaliluku. Seuraavassa luvussa determinantteja käytetään mm. lineaaristen yhtälöryhmien ratkaisemiseen. Tässä vaiheessa sinun on siis keskityttävä siihen, kuinka determinantti lasketaan. Myöhemmin näytetään, mihin näitä determinantteja mm. voidaan käyttää.
5.2.1. Kaksi- ja kolmirivinen determinantti
Opettele ensin luentomonisteen lukujen 2.2.1 ja 2.2.2 esimerkkien ja oppimistehtävien avulla määrittämään 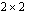 -matriisin ja
-matriisin ja 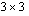 -matriisin determinantti. Jälkimmäisen voit laskea kahdella eri tavalla. Huomaa, että Sarrus'n sääntö pätee vain
-matriisin determinantti. Jälkimmäisen voit laskea kahdella eri tavalla. Huomaa, että Sarrus'n sääntö pätee vain 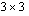 -matriiseille. Tähän tarkoitukseen se kuitenkin on varsin kätevä, ja suosittelenkin tavan opettelemista niin erikoistapaus kuin se onkin.
-matriiseille. Tähän tarkoitukseen se kuitenkin on varsin kätevä, ja suosittelenkin tavan opettelemista niin erikoistapaus kuin se onkin.
Sinun kannattaa myös opetella laskemaan kolmirivinen determinantti sen määritelmän avulla. Kyseisestä määritelmästä ilmenee perusperiaate, jolla determinantti muutetaan astetta pienemmiksi determinanteiksi. Tällä periaatteella määritetään kaikki tätä suuremmat determinantit; asiaa tarkastellaan lähemmin seuraavassa osiossa. Kolmirivisen determinantin määritelmässä determinantti on kehitetty 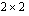 -determinanteiksi sen ensimmäisen rivin suhteen. Tällöin kullakin determinantin ensimmäisen rivin alkiolla kerrotaan vuorotellen kyseisen alkion ns. alideterminantti. Determinantin alkion alideterminentilla tarkoitetaan sitä determinanttia, joka jää, kun determinantista poistetaan kyseisen alkion sisältävät rivi ja sarake. Nämä ensimmäisen rivin kunkin alkion ja sen alideterminantin tulot varustetaan vuorotellen etumerkillä + tai - ja lasketaan lopuksi yhteen.
-determinanteiksi sen ensimmäisen rivin suhteen. Tällöin kullakin determinantin ensimmäisen rivin alkiolla kerrotaan vuorotellen kyseisen alkion ns. alideterminantti. Determinantin alkion alideterminentilla tarkoitetaan sitä determinanttia, joka jää, kun determinantista poistetaan kyseisen alkion sisältävät rivi ja sarake. Nämä ensimmäisen rivin kunkin alkion ja sen alideterminantin tulot varustetaan vuorotellen etumerkillä + tai - ja lasketaan lopuksi yhteen.
5.2.2. Yleinen determinantti
Yleiset determinantit lasketaan siis muuttamalla ne ensin astetta pienemmiksi determinanteiksi. Tätä kehittämistä jatketaan, kunnes päädytään 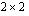 -determinantteihin tai
-determinantteihin tai 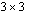 -determinantteihin, jotka lasketaan Sarrus'n säännöllä. Lue luentomonisteen luvusta 2.2.3, kuinka matriisin determinantti kehitetään astetta pienemmiksi determinanteiksi.
-determinantteihin, jotka lasketaan Sarrus'n säännöllä. Lue luentomonisteen luvusta 2.2.3, kuinka matriisin determinantti kehitetään astetta pienemmiksi determinanteiksi.
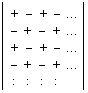
Huomaa, että voit kehittää determinantin astetta pienemmiksi determinanteiksi minkä tahansa rivin tai sarakkeen suhteen. Ennen determinantin laskemista kannattaakin hieman miettiä, mikä olisi tarkoitukseen parhaiten sopiva rivi tai sarake. Sellainen rivi tai sarake, jolla on mahdollisimman paljon nollia, on tietenkin oiva valinta. Kehittäessäsi determinantia valitsemasi rivin tai sarakkeen suhteen kerrot aina kullakin kyseisen rivin tai sarakkeen alkiolla kyseisen alkion alideterminantin, varustat nämä tulot vuorotellen etumerkeillä + ja - sekä lasket ne lopuksi yhteen. Sinun on vain tiedettävä, milloin tulon etumerkiksi tulee + ja milloin -. Itse päättelen tuo etumerkin seuraavan taulukon avulla:
 .
.
Päätettyäni, minkä rivin tai sarakkeen suhteen kehitän determinantin, kuljen taulukon ensimmäistä riviä tai saraketta pitkin kyseisen rivin tai sarakkeen ensimmäisen alkion kohdalle. Kun tiedän, varustetaanko ensimmäinen tulo etumerkillä + vai -, ovat muiden tulojen etumerkit aina vuorotellen + ja -. Jos olen esimerkiksi päättänyt kehittää determinantin neljännen sarakkeen suhteen, kuljen ensin taulukon ensimmäistä riviä seuraavasti: +, -, + ja -. Tiedän nyt, että determinanttia laskettaessa neljännen sarakkeen ensimmäisen alkion ja sen alideterminantin tulo varustetaan etumerkillä - (eli kerrotaan -1:llä) ja tämän jälkeen seuraava tulo varustetaan etumerkillä +, sitten tulee taas - jne.
Käy luentomonisteen esimerkki 2.18 läpi vaihe vaiheelta ja harjoittele determinantin laskemista kehittämällä samainen determinantti jonkun muun rivin tai sarakkeen suhteen. Huomaat, kuinka eri tavoilla päädytään samaan lopputulokseen. Muista olla huolellinen etumerkkien ja laskutoimitusten kanssa. Tee mieluummin liian monta kuin liian vähän välivaiheita. Virheen löytäminen voi näissä tehtävissä joskus olla todella tuskallista.
5.2.3. Determinantin ominaisuuksia
Luentoministeessa on esitetty perusteluineen luettelo determinantin ominaisuuksista. Jos olet kiinnostunut näistä perusteluista, katso ne luentomonisteesta. Voit kuitenkin sivuuttaa ne ja katsoa kyseisten ominaisuuksien luettelon seuraavasta.
Olkoon 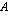
 -matriisi. Matriisin
-matriisi. Matriisin 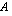 determinantilla
determinantilla 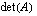 on seuraavat ominaisuudet:
on seuraavat ominaisuudet:
- Jos determinantissa kaksi riviä tai kaksi saraketta vaihdetaan keskenään, determinantti muuttuu vastaluvukseen.
- Jos determinantissa on kaksi samaa riviä tai saraketta, sen arvo on nolla.
- Jos matriisin
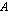 jokin rivi tai sarake kerrotaan luvulla
jokin rivi tai sarake kerrotaan luvulla 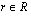 , tällöin
, tällöin 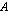 :n determinantti
:n determinantti 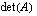 muuttuu
muuttuu 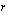 -kertaiseksi.
-kertaiseksi.- Jos matriisin
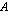 johonkin riviin (tai sarakkeeseen) lisätään sen jokin toinen rivi (tai sarake) kerrottuna reaaliluvulla
johonkin riviin (tai sarakkeeseen) lisätään sen jokin toinen rivi (tai sarake) kerrottuna reaaliluvulla 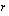 , matriisin determinantti ei muutu.
, matriisin determinantti ei muutu. Luettelon viimeinen ominaisuus on se, jolle on yleensä eniten käyttöä: sen avulla determinantin tiettyyn riviin tai sarakkeeseen voi hankkia lisää nollia determinantin muuttumatta. Tämän jälkeen determinantti on helppo kehittää kyseisen rivin tai sarakkeen suhteen.
Testaa lopuksi oheisella testaa tietosi -tehtävällä, että osaat määrittää matriisin determinantin.
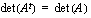

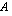 jokin rivi tai sarake on pelkkä nollavektori, on
jokin rivi tai sarake on pelkkä nollavektori, on 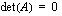 .
.