[edellinen] [sisällys] [seuraava]
2.7. Juuriyhtälö
Juuriyhtälöiksi nimitetään yhtälöitä, jotka sisältävät juurilausekkeita. Esimerkiksi
on juuriyhtälö. Tällainen juurilausekkeita sisältävä yhtälö ratkaistaan yleensä korottamalla se puolittain neliöön. Yhtälön molempien puolien neliöönkorottaminen ei kuitenkaan ole ongelmatonta, kuten seuraavasta tarkastelusta ilmenee.
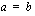 .
.
Esittäkööt symbolit 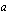 ja
ja 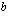 nyt juuriyhtälön vasenta ja oikeaa puolta. Kun yhtälön vasen ja oikea puoli on korotettu neliöön, se tulee muotoon
nyt juuriyhtälön vasenta ja oikeaa puolta. Kun yhtälön vasen ja oikea puoli on korotettu neliöön, se tulee muotoon
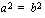 .
.
Mietitäänpä nyt, milloin neliöönkorotuksella aikaansaatu yhtälö 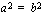 toteutuu. Lukujen neliöt ovat yhtäsuuret silloin, kun luvut ovat yhtäsuuret tai luvut ovat toistensa vastalukuja. Yhtälö
toteutuu. Lukujen neliöt ovat yhtäsuuret silloin, kun luvut ovat yhtäsuuret tai luvut ovat toistensa vastalukuja. Yhtälö 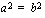 toteutuu siis silloin, kun
toteutuu siis silloin, kun 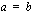 tai
tai 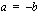 . Tämä merkitsee sitä, että neliöönkorotuksella aikaansaatu yhtälö toteuttaa alkuperäisen yhtälön
. Tämä merkitsee sitä, että neliöönkorotuksella aikaansaatu yhtälö toteuttaa alkuperäisen yhtälön 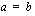 sekä uuden yhtälön
sekä uuden yhtälön 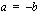 . Neliöönkorotuksella saadulla yhtälöllä voi tästä syystä olla ylimääräisiä ratkaisuja, jotka eivät toteuta alkuperäistä yhtälöä
. Neliöönkorotuksella saadulla yhtälöllä voi tästä syystä olla ylimääräisiä ratkaisuja, jotka eivät toteuta alkuperäistä yhtälöä 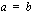 , vaan yhtälön
, vaan yhtälön 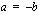 .
.
Kuinka tämä neliöönkorotuksella saatujen ylimääräisten ratkaisujen ongelma sitten ratkaistaan? Valittavana on kaksikin vaihtoehtoa: yhtälön ratkaisija voi aina ratkaista ensin neliöönkorotuksella saamansa yhtälön ja testata lopuksi kunkin saamansa ratkaisuvaihtoehdon, toteuttaako se alkuperäisen yhtälön vai ei. Sijoittamalla vuorotellen jokaisen saamansa ratkaisuvaihtoehdon alkuperäiseen yhtälöön voi hylätä niistä ne, jotka eivät sitä toteuta. Tämä on ihan hyvä tapa ratkaista neliöönkorotuksen tuomien ylimääräisten ratkaisujen ongelma. Ainoastaan silloin vaihtoehto tuntuu ikävältä, kun sijoitettavaksi tulee hankalia 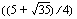 :n kaltaisia lausekkeita.
:n kaltaisia lausekkeita.
Toinen vaihtoehto näiden ylimääräisten ratkaisujen ongelmaan on käyttää tietoa:
Jos 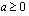 ja
ja 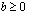 , niin
, niin 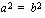 silloin ja vain silloin, kun
silloin ja vain silloin, kun 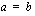 .
.
Silloin, kun yhtälön molemmat puolet ovat ei-negatiiviset, ei neliöönkorottaminen muuta yhtälön ratkaisuja, vaan neliöönkorotuksella aikaansaadulla yhtälöllä on täsmälleen samat ratkaisut kuin alkuperäiselläkin yhtälöllä. Tämä tunnetaan ns. neliöönkorotusehtona, jonka mukaan yhtälö (ja epäyhtälö) voidaan korottaa puolittain neliöön, jos sen molemmat puolet ovat ei-negatiiviset.
Luentomonisteessa esitellään juuriyhtälön ratkaisemista luvussa 2.7.1. Esimerkissä 2.22 havainnollistetaan juuriyhtälön ratkaisuvaiheita. Huomaa esimerkkiä lukiessasi seuraavat seikat:
- Juuriyhtälö on ensin muutettava muotoon, jossa sen korottaminen puolittain neliöön on järkevintä. Esimerkiksi yhtälöä
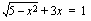 ei kannata korottaa puolittain neliöön. Yhtälön neliöönkorottaminen tarkoittaa sitä, että korotetaan vasen puoli neliöön ja oikea puoli neliöön. Jos näin tehtäisiin em. yhtälölle, päädyttäisiin seuraavanlaiseen yhtälöön (muista summan neliön muistikaava, joka opetettiin modulissa 1):
ei kannata korottaa puolittain neliöön. Yhtälön neliöönkorottaminen tarkoittaa sitä, että korotetaan vasen puoli neliöön ja oikea puoli neliöön. Jos näin tehtäisiin em. yhtälölle, päädyttäisiin seuraavanlaiseen yhtälöön (muista summan neliön muistikaava, joka opetettiin modulissa 1): Uusi yhtälö on hankalamman näköinen kuin edellinen eikä juurilausekkeesta päästy eroon. Neliöönkorottamista varten yhtälö kannattaa muokata muotoon, jossa juurilauseke on yksin omalla puolellaan yhtälöä. Tällöin juurilausekkeen neliö on sama kuin juurrettava eli juurilauseke häviää neliöönkorotuksessa. Esimerkkitapauksessamme juurilausekkeesta päästään eroon seuraavasti:
- Neliöjuuri on määritelty vain ei-negatiivisille luvuille. Esimerkissämme
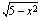 on määritelty, kun juurrettava
on määritelty, kun juurrettava 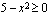 , joka toteutuu, kun
, joka toteutuu, kun 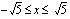 .
. - Kun juuriyhtälö on muutettu muotoon, jossa juurilauseke on yksin omalla puolellaan, ja on huomioitu sekä juuren määrittelyehto että juuren arvon positiivusuusehto, ovat yhtälön molemmat puolet ei-negatiiviset eli neliöönkorotusehto on voimassa. Ennen kuin jatkat tästä vaiheesta, mieti vielä, mitkä luvut toteuttavat nuo molemmat ehdot. Esimerkkitapauksessamme on oltava voimassa
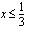 ja
ja 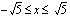 . Nämä molemmat toteutuvat, kun
. Nämä molemmat toteutuvat, kun 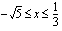 . Neliöönkorotuksen jälkeen saadun yhtälön ratkaisuista hyväksytään vain ne, jotka toteuttavat tämän ehdon. Huomaa, että neliöönkorotusehto huomioiden sinun ei tarvitse sijoittaa saamiasi ratkaisuvaihtoehtoja vuorotellen alkuperäiseen yhtälöön, vaan riittää, että katsot, mitkä niistä kuuluvat tuolle määrittelyvälille.
. Neliöönkorotuksen jälkeen saadun yhtälön ratkaisuista hyväksytään vain ne, jotka toteuttavat tämän ehdon. Huomaa, että neliöönkorotusehto huomioiden sinun ei tarvitse sijoittaa saamiasi ratkaisuvaihtoehtoja vuorotellen alkuperäiseen yhtälöön, vaan riittää, että katsot, mitkä niistä kuuluvat tuolle määrittelyvälille. Käy nyt esimerkki 2.22 huolellisesti läpi vaihe vaiheelta niin, että ymmärrät, miksi kussakin vaiheessa on toimittu kyseisellä tavalla. Harjoittele sen jälkeen juuriyhtälön ratkaisemista seuraavan oppimistehtävän avulla.
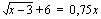
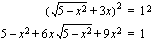
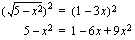
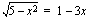
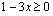 eli
eli 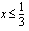 .
. 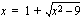 .
.