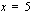Juurilauseke on määritelty, kun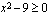 
eli 
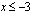tai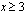 
. Koska neliöjuuren arvo on aina positiivinen tai nolla, on lisäksi oltava voimassa 
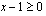eli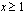 
. Nämä molemmat ehdot toteutuvat, kun 
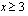. Tällöin myös yhtälön neliöönkorotusehto on voimassa. Korotetaan yhtälön vasen ja oikea puoli neliöön ja ratkaistaan näin saatu yhtälö.
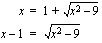
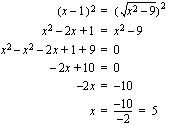
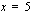toteuttaa ehdon 
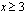, joten se on alkuperäisen yhtälön ratkaisu. 