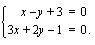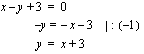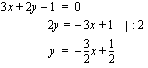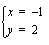[edellinen] [sisällys] [seuraava]
2.3. Yhtälöpari
Ensimmäisen asteen yhtälöpari muodostuu kahdesta suoran yhtälöstä. Se voidaan esittää muodossa
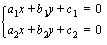, missä 
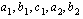ja 
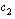ovat vakioita.
Yhtälöparia ratkaistaessa etsitään ne muuttujien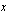 
ja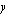 
arvot, jotka toteuttavat molemmat yhtälöparin yhtälöt.
Yhtälöparin voi ratkaista graafisesti piirtämällä molemmat yhtälöiden esittämät suorat samaan koordinaatistoon ja katsomalla näiden suorien leikkauspisteen. Havainnollistakoon seuraava esimerkki tätä ratkaisutapaa.
Esimerkki 2.12.
Ratkaise graafisesti yhtälöpari
Yhtälö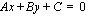 
esittää suoraa aina, kun vakioista 
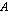ja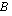 
ainakin toinen on nollasta poikkeava. Olemme oppineet piirtämään suoran, kun sen yhtälö on muotoa 
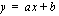. Tämä on suoran yhtälön ns. ratkaistu muoto. Kun suoran yhtälö on kirjoitettu muotoon 
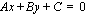, sanotaan, että se on esitetty ns. yleisessä muodossa. Mikäli suoran yhtälö on annettu yleisessä muodossa, se kannattaa piirtämistä varten muuttaa ratkaistuun muotoon. Tämä tapahtuu yksinkertaisesti ratkaisemalla 
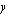tästä yhtälöstä. Tässä tapauksessa suoran yhtälöiden yleisistä muodoista päädytään ratkaistuihin muotoihin seuraavasti:
Piirretään saadut suorat samaan koordinaatistoon ja katsotaan suorien leikkauspiste.
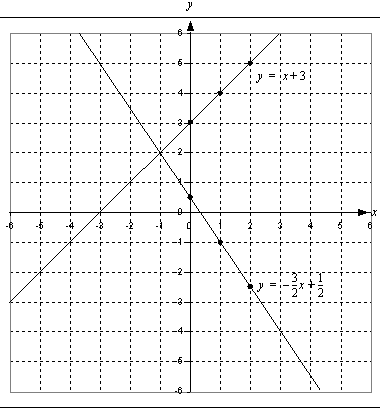
Kuviosta nähdään, että yhtälöparin suorat leikkaavat pisteessä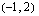 
.
Koska kahdella suoralla voi olla leikkauspisteitä yksi (suorat erisuuntaiset), ei yhtään (suorat yhdensuuntaiset ja erilliset) tai äärettömän monta (itse asiassa samat suorat), voi ensimmäisen asteen yhtälöparillakin olla ratkaisuja yksi, ei yhtään tai äärettömän monta. Tätä on havainnollistettu kuvalla luentomonisteen sivulla 61. Seuraavaksi sinun kannattaakin lukea luentomonisteen luvusta 3.2.1, mitä siellä on kerrottu yhtälöparista ja sen ratkaisemisesta algebrallisesti eli laskemalla. Käy huolella läpi esimerkit molemmista ratkaisutavoista (sijoituskeino ja yhteenlaskukeino). Lopuksi voit vielä harjoitella yhtälöparin ratkaisemista oheisella oppimistehtävällä, ennen kuin siirryt varsinaisiin harjoituksiin.
