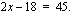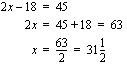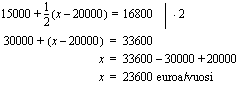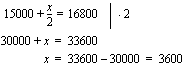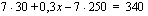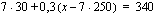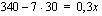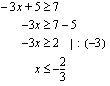[edellinen] [sisällys] [seuraava]
2.2. Ensimmäisen asteen yhtälö ja epäyhtälö
Yhtälöt on jaettu eri tyyppeihin niissä esiintyvien funktioiden perusteella. Koska ensimmäisen asteen yhtälö liittyy 1. asteen polynomifunktioon, on meidän syytä tutustua aluksi tähän funktioon.
2.2.1. Ensimmäisen asteen polynomifunktio
Ensimmäisen asteen polynomifunktio on muotoa
Esimerkiksi 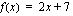 ja
ja 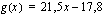 ovat ensimmäisen asteen polynomifunktioita. Ensimmäisen asteen polynomifunktion kuvaaja on suora. Edellä harjoiteltiin jo suoran piirtämistä. Muista, että voit aina piirtää suoran kahdella eri tavalla: joko laskemalla siltä muutaman pisteen suoran yhtälön avulla tai käyttämällä seuraavia tietoja:
ovat ensimmäisen asteen polynomifunktioita. Ensimmäisen asteen polynomifunktion kuvaaja on suora. Edellä harjoiteltiin jo suoran piirtämistä. Muista, että voit aina piirtää suoran kahdella eri tavalla: joko laskemalla siltä muutaman pisteen suoran yhtälön avulla tai käyttämällä seuraavia tietoja:
Ensimmäisen asteen polynomifunktiolla voidaan kuvata hyvin monia erilaisia reaalimaailman ilmiöitä. Seuraavassa esimerkissä on yksi tällainen.
Esimerkki 2.2.
Paavolan tilan lihanjalostamo ostaa lähiseudun tuottajilta lihaa ja purkittaa sen Paavolan lihaherkuksi. Tilalla tiedetään, että yhden lihasäilykepurkin tuotanto- ja raaka-ainekustannukset ovat 3 euroa. Lisäksi tuotantolaitteiden ja -tilojen pääomakustannukset ovat 210 euroa kuukaudessa. Kuukausittain Paavolan tilalla otetaan 4 lihasäilykepurkkia omaan käyttöön, loput tulevat myyntiin alueen elintarvikeliikkeisiin. Liikkeet maksavat lihaherkusta 5 euroa purkilta.
Muodosta funktio, joka ilmoittaa Paavolan tilan lihan purkituksesta ja säilykkeen myynnistä saaman kuukausittaisen tuoton kuukaudessa tuotetun lihasäilykepurkkimäärän funktiona. Piirrä tämän funktion kuvaaja.
Olkoon muuttuja 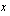 tilalla kuukaudessa tuotettu säilykepurkkimäärä. Pyritään ilmoittamaan tilan saama kuukausittainen tuotto tämän muuttujan avulla. Koska
tilalla kuukaudessa tuotettu säilykepurkkimäärä. Pyritään ilmoittamaan tilan saama kuukausittainen tuotto tämän muuttujan avulla. Koska
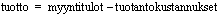 ,
,
voidaan aloittaa muodostamalla ensin muuttujan avulla myyntitulojen ja tuotantokustannusten lauseke. Myyntiin tulee lihasäilykepurkkeja 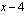 kpl, koska 4 purkkia otettiin kuukausittain omaan käyttöön. Koska ne myydään hintaan 5 euroa/kpl, ovat purkkien myynnistä saadut myyntitulot
kpl, koska 4 purkkia otettiin kuukausittain omaan käyttöön. Koska ne myydään hintaan 5 euroa/kpl, ovat purkkien myynnistä saadut myyntitulot 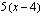 euroa/kk. Tuotantokustannukset olivat 3 euroa/kpl ja lisäksi 210 euroa/kk eli yhteensä
euroa/kk. Tuotantokustannukset olivat 3 euroa/kpl ja lisäksi 210 euroa/kk eli yhteensä 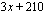 euroa/kk. Kuukausittainen tuotto on siten
euroa/kk. Kuukausittainen tuotto on siten
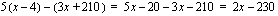 .
.
On huomattava, että muuttujan 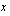 ollessa suure, jonka yksikkö on kpl/kk, eivät tämän funktion määrittelyssä olevat vakiot 2 ja -230 ole reaalilukuja, vaan ve ovat myös suureita, joilla on oma mittayksikkö. Vakiolla 2 on oltava sellainen mittayksikkö, että kerrottaessa se suureella
ollessa suure, jonka yksikkö on kpl/kk, eivät tämän funktion määrittelyssä olevat vakiot 2 ja -230 ole reaalilukuja, vaan ve ovat myös suureita, joilla on oma mittayksikkö. Vakiolla 2 on oltava sellainen mittayksikkö, että kerrottaessa se suureella 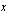 kpl/kk saadaan tulokseksi
kpl/kk saadaan tulokseksi 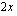 euroa/kk. Vakion 2 mittayksikkö on siten euroa/kpl ja se ilmoittaa yhden purkin myynnistä saatavan tuoton. Vakion -230 yksikön on oltava kuukausittaisen tuoton yksikkö eli euroa/kk. Tämä vakio voidaan tulkita kiinteiksi kustannuksiksi. Mittayksiköiden avulla ilmaistuna Paavolan tilan kuukausittaisen tuoton ilmoittaa funktio
euroa/kk. Vakion 2 mittayksikkö on siten euroa/kpl ja se ilmoittaa yhden purkin myynnistä saatavan tuoton. Vakion -230 yksikön on oltava kuukausittaisen tuoton yksikkö eli euroa/kk. Tämä vakio voidaan tulkita kiinteiksi kustannuksiksi. Mittayksiköiden avulla ilmaistuna Paavolan tilan kuukausittaisen tuoton ilmoittaa funktio
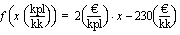 .
.
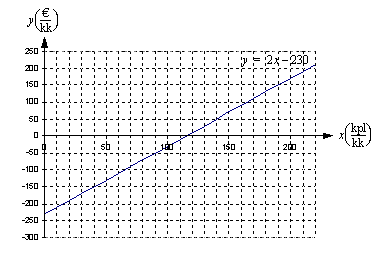
Piirretään vielä lopuksi tuon funktion kuvaajasuora. Lasketaan suoralta taulukoimalla muutama piste:
Mikäli olette jo selanneet enemmänkin matematiikan propedeuttisen kurssin luentomonistetta, olette havainneet, että esitän sovellusesimerkeissä funktiot aina mittayksiköllisinä. Olen tehnyt näin, jotta samalla ilmenisi, mitä funktioissa esiintyvät vakiot ovat reaalimaailmassa. Jos esimerkiksi yrityksen tuotantokustannukset esitetään kuukausittaisen tuotantomäärän 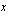 funktiona muodossa
funktiona muodossa  , ei lukija tule välttämättä ajatelleeksi, mitä vakiot 24 ja 208 funktion määrittelyssä tarkoittavat. Sen sijaan esitettäessä funktio muodossa
, ei lukija tule välttämättä ajatelleeksi, mitä vakiot 24 ja 208 funktion määrittelyssä tarkoittavat. Sen sijaan esitettäessä funktio muodossa
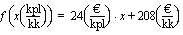 ,
,
lukija näkee heti yksiköistä, että 24 tarkoittaa yksikkökustannuksia ja 208 kuukausittaisia kiinteitä kustannuksia. Kun tällaisella funktiolla mallitetaan todellista tilannetta, nuo vakiot saadaan määritettyä esimerkiksi yrityksen tilastojen avulla.
Tapani esittää sovellusesimerkkien funktiot mittayksiköllisinä ei ole hyvä laskuissa. Ratkoessanne tällaisia sovellustehtäviä teidän kannattaakin jättää mittayksiköt pois. Tämä on helppoa, koska olen kirjoittanut mittayksiköt aina sulkeisiin: voitte yksinkertaisesti "pudottaa" nuo suluissa olevat yksiköt pois, jolloin esimerkiksi edellinen funktio tulee muotoon 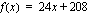 . Mittayksiköllinen muoto on esimerkeissä sitä varten, että voitte yksikön avulla tulkita, mitä mittayksikkö tarkoittaa todellisuudessa.
. Mittayksiköllinen muoto on esimerkeissä sitä varten, että voitte yksikön avulla tulkita, mitä mittayksikkö tarkoittaa todellisuudessa.
2.2.2. Ensimmäisen asteen yhtälö
Muuttujan 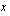 ensimmäisen asteen yhtälö voidaan aina sieventää muotoon
ensimmäisen asteen yhtälö voidaan aina sieventää muotoon
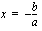 .
.
- Jos
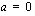 ja
ja 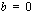 , yhtälö on muotoa
, yhtälö on muotoa 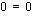 ja sanotaan, että yhtälö on tällöin identtisesti tosi, mikä tarkoittaa, että se toteutuu muuttujan
ja sanotaan, että yhtälö on tällöin identtisesti tosi, mikä tarkoittaa, että se toteutuu muuttujan 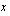 kaikilla reaaliarvoilla.
kaikilla reaaliarvoilla. - Jos
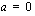 ja
ja 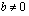 , yhtälö tulee muotoon
, yhtälö tulee muotoon 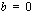 , mikä on epätosi. Tällöin yhtälön sanotaan olevan identtisesti epätosi, eikä se toteudu millään muuttujan
, mikä on epätosi. Tällöin yhtälön sanotaan olevan identtisesti epätosi, eikä se toteudu millään muuttujan 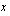 arvolla. Yhtälöllä ei ole tällöin lainkaan ratkaisua.
arvolla. Yhtälöllä ei ole tällöin lainkaan ratkaisua. Käytännössä ensimmäisen asteen yhtälön tunnistaa siitä, että yhtälössä ei esiinny muuttujan potensseja, eikä muuttuja esiinny nimittäjässä.
Ne teistä, joille ensimmäisen asteen yhtälön ratkaiseminen on tuttua ja hyvässä muistissa, voitte lukaista kertauksen vuoksi luentomonisteesta luvun 2.2.1 ja jatkaa ensimmäisen asteen epäyhtälön parissa luvusta 2.2.3 sivulta 53. Niiden, jotka tarvitsevat enemmän opastavaa kertausta, kannattaa jatkaa tämän tutorointipaketin avulla.
Esimerkki 2.3.
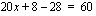 .
.
Tämän jälkeen siirretään yhtälön termejä (yhtenlaskettavia) siten, että muuttujan sisältävät termit tulevat yhtälön toiselle ja vakiot sen toiselle puolelle. On muistettava, että termin vaihtaessa puolta, sen etumerkki vaihtuu. Termien siirtämisen jälkeen suoritetaan yhtälön kummallakin puolella merkityt laskutoimitukset.
Esimerkki 2.4.
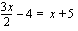 .
.
Jos yhtälö sisältää nimittäjiä, ne kannattaa poistaa heti aluksi kertomalla yhtälö puolittain nimittäjien pienimmällä yhteisellä jaettavalla. Tällöin yhtälön jokainen termi kerrotaan kyseisellä luvulla. Aloitetaan tässä kertomalla yhtälön kaikki termit luvulla 2.
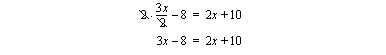
Tämän jälkeen siirretään termit, suoritetaan merkityt laskutoimitukset ja jaetaan tarvittaessa yhtälö puolittain tuntemattoman kertoimella.
Esimerkki 2.6.
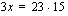 ,
,
jossa verrannon ristitulot on merkitty yhtäsuuriksi. Ratkaistaan tämä jakamalla yhtälö puolittain tuntemattoman kertoimella 3.
Oppimistehtävä 2.7.
Pelkästä mekaanisesta yhtälön ratkaisutaidosta ei ole suurta hyötyä arkielämässä. Sen sijaan taito käyttää yhtälöitä erilaisten sanallisten ongelmien ratkaisemiseen on hyödyksi esimerkiksi monenlaisissa arki- ja talouselämän ongelmatilanteissa. Mitä enemmän hallitset yhtälöiden käyttöä sitä enemmän osaat hyötyä taidostasi. Sanallisen ongelman muotoileminen matemaattiseen muotoon esimerkiksi yhtälöksi ei kuitenkaan ole aivan helppoa. Taito vaatii harjaantumista. Seuraava osio on tarkoitettu sinulle opastukseksi tämän matemaattisen mallittamisen taidon kehittämistä varten.
Esimerkki 2.8.
Maija myy kesätorilla äitinsä poimimia mustikoita. Hän joutuu maksamaan myyntipöydästä vuokraa 10 euroa/myyntipäivä. Mustikat hän myy hintaan 2 euroa/l. Lisäksi hän veloittaa myyntityöstä 8 euroa/päivä. Loput myyntitulot jäävät hänen äidilleen. Kuinka monta litraa mustikoita Maijan äidin pitäisi poimia päivittäin myyntiin, jotta hän saisi myyntituloja 45 euroa päivässä?
Kokeillaan, kuinka Maijan ongelma ratkeaa yhtälön avulla. Tällöin on ensin pystyttävä kirjoittamaan ongelmasta yhtälö, jonka muodostaminen tapahtuu vaiheittain. Sinun ei tarvitse osata muodostaa sitä heti alusta loppuun oikein. Ensimmäinen vaihe on päättää, mikä on yhtälön tuntematon suure. Tässä kysyttiin päivässä poimittavaa mustikkamäärää litroina, joten valitaan se muuttujaksi 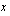 .
.
Perusidea yhtälön muodostamisessa on ilmoittaa sama asia kahdella eri tavalla. Yhtälö muodostuu, kun ne merkitään yhtäsuuriksi. Esimerkiksi tässä tapauksessa voimme ilmoittaa Maijan äidin päivittäiset myyntitulot kahdella eri tavalla. Tavoitteena oli, että ne ovat 45 euroa/päivä. Toisaalta hänelle jäävät myyntitulot muodostuvat, kun mustikoiden myynnistä saadusta summasta vähennetään kulut eli pöydän vuokra ja Maijan palkkio. Kun Maija myy 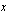 l mustikoita hintaan 2 euroa/l, kertyy myynnistä
l mustikoita hintaan 2 euroa/l, kertyy myynnistä 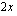 euroa. Kulut ovat yhteensä 18 euroa, joten Maijan äidille marjojen myynnistä jää
euroa. Kulut ovat yhteensä 18 euroa, joten Maijan äidille marjojen myynnistä jää 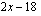 euroa. Ratkaistavaksemme jäävä yhtälö saadaan, kun merkitään äidin myyntitulot ja haluttu tavoite yhtäsuuriksi:
euroa. Ratkaistavaksemme jäävä yhtälö saadaan, kun merkitään äidin myyntitulot ja haluttu tavoite yhtäsuuriksi:
Muista, että tämäkin tulos kannattaa tarkistaa. Sijoittaminen muodostettuun yhtälöön ei riitä virheen paljastamiseksi. Jos yhtälö on väärin eli se ei vastaakaan annettua ongelmaa, ei tuloskaan voi olla oikein, vaikka yhtälö olisikin oikein ratkaistu. Sinun täytyy kokeilla saamaasi tulosta alkuperäiseen ongelmaan ja testata, toteuttaako ratkaisusi sen. Vastaukseksi saamallamme litramäärällä kertyy mustikoiden myynnistä 63 euroa/päivä. Kun tästä vähennetään kulut 18 euroa, jää toivottu 45 euroa/päivä.
Esimerkki 2.9.
Matti joutuu maksamaan tuloistaan neljänneksen veroa 20000 euron vuosituloon saakka. Tämän rajatulon ylittävästä osasta hänen on maksettava jo puolet veroa. Kuinka suuret pitäisi Matin vuotuisten bruttotulojen olla, jotta hänen nettovuosiansionsa olisi 16800 euroa?
Koska Matti maksaa 20000 euron ansioista veroa 5000 euroa, jää niistä nettotuloiksi 15000 euroa. Matin tulojen on siis ylitettävä 20000 euroa/vuosi. Ratkaistaan tehtävä yhtälön avulla. Esitän kaksi erilaista tapaa, jotta huomaatte, että yhtä ainoaa oikeaa tapaa tällaisten tehtävien ratkaisuun ei ole.
Merkitään muuttujalla 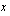 kysyttyä bruttovuosiansiota, joka on enemmän kuin 20000 euroa/vuosi. Tiedämme, että tästä rajatulosta jää veron maksun jälkeen 15000 euroa/vuosi. Ylimenevä osa on
kysyttyä bruttovuosiansiota, joka on enemmän kuin 20000 euroa/vuosi. Tiedämme, että tästä rajatulosta jää veron maksun jälkeen 15000 euroa/vuosi. Ylimenevä osa on 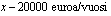 . Siitä menee veroa puolet, jolloin puolet jää nettotuloksi. Asetetaan muuttujan avulla ilmoitettu nettovuosiansio yhtä suureksi kuin tavoite ja ratkaistaan saatu yhtälö.
. Siitä menee veroa puolet, jolloin puolet jää nettotuloksi. Asetetaan muuttujan avulla ilmoitettu nettovuosiansio yhtä suureksi kuin tavoite ja ratkaistaan saatu yhtälö.
Merkitään nyt muuttujalla 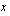 rajatulon 20000 euroa/vuosi ylittävää osaa. Siitä jää nettotuloksi puolet, jolloin nettotulot ovat yhteensä
rajatulon 20000 euroa/vuosi ylittävää osaa. Siitä jää nettotuloksi puolet, jolloin nettotulot ovat yhteensä 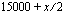 . Merkitään jälleen tämän muuttujan avulla ilmaistu nettoansio yhtä suureksi kuin tavoite ja ratkaistaan näin saatu yhtälö.
. Merkitään jälleen tämän muuttujan avulla ilmaistu nettoansio yhtä suureksi kuin tavoite ja ratkaistaan näin saatu yhtälö.
Kuinka olisit itse ratkaissut nämä tehtävät? Olisitko käyttänyt esimerkin tavoin yhtälöä vai päätellyt ratkaisun? Itse ratkaisen tämän tyyppiset tehtävät useimmiten päättelemällä. Esimerkkien kaltaiset yksinkertaiset tilanteet ovat kuitenkin hyviä yhtälöiden muodostamisen harjoitteluun. Ongelmien vaikeutuessa päättelytaito ei enää riitä. Silloin yhtälöt ovat hyvä apuväline tilanteen vaatimassa päätöksenteossa.
Ennen kuin harjoittelet itse ongelman ratkaisemista yhtälön avulla, tarkista seuraavan testaa tietosi -tehtävän avulla valmiutesi muodostaa matemaattisia lausekkeita annetusta ongelmasta.
Testaa tietosi II
Autovuokraamo perii perusmaksua 30 euroa/vrk, joka sisältää 250 km. Tämän yli menevältä kilometrimäärältä se veloittaa 0,30 euroa/km. Liisa pohtii, kuinka pitkälle viikon kestävälle matkalle 340 euroa riittää.
Mikä tai mitkä seuraavista yhtälöistä antaisivat ratkaisun Liisan ongelmaan? Mieti myös, miksi loput yhtälöt ovat väärin.
Yritä ratkaista seuraava tehtävä yhtälön avulla. Mieti myös, millä tavoin itse ratkaisisit tehtävän, jos saisit vapaasti valita ratkaisutavan.
2.2.3. Ensimmäisen asteen epäyhtälö
Ensimmäisen asteen epäyhtälö voidaan aina sieventää muotoon
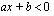 , missä
, missä 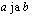 ovat vakioita.
ovat vakioita.
Epäyhtälömerkin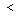 tilalla voi tietenkin olla mikä tahansa muu merkeistä
tilalla voi tietenkin olla mikä tahansa muu merkeistä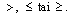 Ensimmäisen asteen epäyhtälö ratkaistaan kuten ensimmäisen asteen yhtälö. Ainoa poikkeus on se, että kerrottaessa tai jaettaessa epäyhtälö puolittain negatiivisella luvulla, epäyhtälömerkin suunta vaihtuu. Esimerkiksi:
Ensimmäisen asteen epäyhtälö ratkaistaan kuten ensimmäisen asteen yhtälö. Ainoa poikkeus on se, että kerrottaessa tai jaettaessa epäyhtälö puolittain negatiivisella luvulla, epäyhtälömerkin suunta vaihtuu. Esimerkiksi:
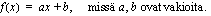
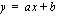 kulmakerroin on
kulmakerroin on 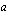 . Kulmakerroin määrää suoran suunnan:
. Kulmakerroin määrää suoran suunnan: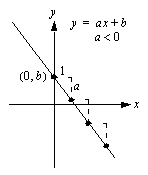
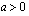 , suora on nouseva,
, suora on nouseva,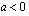 , suora on laskeva ja
, suora on laskeva ja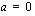 , suora on
, suora on 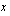 -akselin suuntainen.
-akselin suuntainen.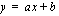 leikkaa
leikkaa 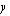 -akselin pisteessä
-akselin pisteessä 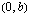 .
.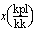
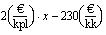
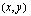
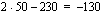
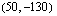
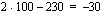
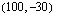
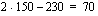
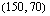
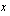 (kpl/kk) funktiona on
(kpl/kk) funktiona on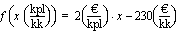 .
. 
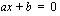 , missä
, missä 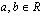 .
.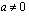 , yhtälöllä on täsmälleen yksi ratkaisu
, yhtälöllä on täsmälleen yksi ratkaisu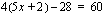 .
.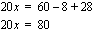
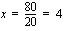
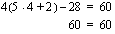
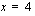
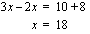
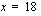
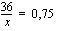 .
.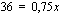 .
.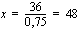
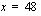
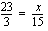 .
.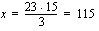
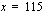
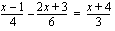 .
.