[edellinen] [sisällys] [seuraava]
1.7. Funktio
Erilaiset funktiot ja niiden tutkiminen on yksi tämän kurssin perusasioita. Tästä syystä on tärkeää, että jo tässä johdantojaksossa opit tietämään, mikä on funktio ja miten sen kuvaaja piirretään. Funktioilla kuvataan suureiden välisiä riippuvuussuhteita. Funktio voi esimerkiksi ilmoittaa, kuinka henkilön nettopalkka riippuu bruttopalkasta, kuinka äitiyspäiväraha riippuu vuosituloista, kuinka tuotantokustannukset riippuvat tuotantomäärästä tai kuinka jonkun tuotteen menekki riippuu sen hinnasta jne. Funktioita siis käytetään kuvaamaan erilaisia reaalimaailmassa ilmeneviä suureiden välisiä riippuvuussuhteita. Funktioilla esitetään matemaattisia malleja todellisuudesta: mm. taloustieteilijät käyttävät niitä mallittaessaan erilaisia talouden ilmiöitä ja tehdessään päätöksiä näiden matemaattisten mallien avulla.
1.7.1. Funktion määritelmä
Voit aloittaa lukemalla, mitä kurssimonisteessa sanotaan funktion määritelmästä sekä käydä läpi kohdan pari esimerkkiä.
Koska funktioilla kuvataan suureiden välisiä riippuvuussuhteita, ne voidaan ajatella säännöiksi, jotka ilmoittavat, kuinka tietty suure riippuu tietystä muuttujasta, esimerkiksi kuinka tuotantokustannukset riippuvat tuotetusta määrästä. Mikä tahansa sääntö ei kuitenkaan ole funktio. Jotta sääntö, joka liittää jonkin muuttujan arvoihin tietyn suureen arvoja, olisi funktio, on tämän säännön oltava yksikäsitteinen. Tämä yksikäsitteisyysvaatimus tarkoittaa, että jokaista muuttujan arvoa on vastattava täsmälleen yksi funktion arvo. Suureiden välistä riippuvuutta kuvaavat funktiot voidaan yleensä ilmaista matemaattisina lausekkeina, mutta funktio voi olla mikä tahansa muukin sääntö, kunhan tuo yksikäsitteisyysvaatimus toteutuu. Esimerkiksi sääntö 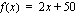 määrittää yksikäsitteisesti, mikä on reaalilukua
määrittää yksikäsitteisesti, mikä on reaalilukua 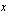 (muuttuja) vastaava funktion arvo. Tuo funktio voisi ilmoittaa, kuinka tuotantokustannukset riippuvat tuotantomäärästä
(muuttuja) vastaava funktion arvo. Tuo funktio voisi ilmoittaa, kuinka tuotantokustannukset riippuvat tuotantomäärästä  , kun yksikkökustannukset ovat 2 euroa/kpl ja kiinteät tuotantokustannukset 50 euroa. Sääntö
, kun yksikkökustannukset ovat 2 euroa/kpl ja kiinteät tuotantokustannukset 50 euroa. Sääntö 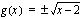 sen sijaan ei määrittele funktiota, koska tiettyä muuttujan arvoa
sen sijaan ei määrittele funktiota, koska tiettyä muuttujan arvoa 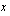 ei vastaa täsmälleen yksi funktion arvo, vaan niitä on kaksi erilaista:
ei vastaa täsmälleen yksi funktion arvo, vaan niitä on kaksi erilaista: 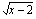 ja
ja 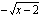 .
.
Funktio 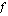 voidaan siis ajatella yksikäsitteiseksi säännöksi joltakin joukolta
voidaan siis ajatella yksikäsitteiseksi säännöksi joltakin joukolta 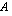 jollekin joukolle
jollekin joukolle 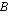 ja tätä funktiota merkitään:
ja tätä funktiota merkitään: 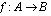 . Jos tällä funktiolla kuvataan, kuinka tietyn suureen arvot riippuvat tietystä muuttujasta, muodostavat nuo muuttujan arvot joukon
. Jos tällä funktiolla kuvataan, kuinka tietyn suureen arvot riippuvat tietystä muuttujasta, muodostavat nuo muuttujan arvot joukon 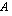 ja tuon suureen arvot joukon
ja tuon suureen arvot joukon 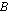 . Matemaattisissa esimerkeissä nuo joukot ovat usen lukujoukkoja, esimerkiksi reaalilukujen osajoukkoja, reaalimaailman ilmiöitä kuvaavissa esimerkeissä nuo joukot voivat koostua mistä tahansa suureiden arvoista. Funktion muuttujien joukkoa
. Matemaattisissa esimerkeissä nuo joukot ovat usen lukujoukkoja, esimerkiksi reaalilukujen osajoukkoja, reaalimaailman ilmiöitä kuvaavissa esimerkeissä nuo joukot voivat koostua mistä tahansa suureiden arvoista. Funktion muuttujien joukkoa 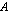 sanotaan funktion lähtö- tai määrittelyjoukoksi ja sille käytetään merkintää
sanotaan funktion lähtö- tai määrittelyjoukoksi ja sille käytetään merkintää 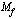 . Meidän esimerkeissämme määrittelyjoukko on yleensä laajin mahdollinen reaalilukujen osajoukko, jossa funktion lauseke on määritelty. Maalijoukko
. Meidän esimerkeissämme määrittelyjoukko on yleensä laajin mahdollinen reaalilukujen osajoukko, jossa funktion lauseke on määritelty. Maalijoukko 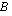 on se joukko, josta funktio saa arvoja. Matemaattisissa esimerkeissä tällä kurssilla tuo joukko on yleensä
on se joukko, josta funktio saa arvoja. Matemaattisissa esimerkeissä tällä kurssilla tuo joukko on yleensä 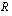 . Funktion
. Funktion 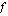 arvojen joukkoa sanotaan funktion arvojoukoksi, jolle käytetään merkitää
arvojen joukkoa sanotaan funktion arvojoukoksi, jolle käytetään merkitää 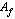 . Funktion arvojoukko voi olla koko joukko
. Funktion arvojoukko voi olla koko joukko 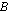 tai jokin sen osajoukko. Esimerkiksi funktion
tai jokin sen osajoukko. Esimerkiksi funktion 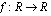 ,
, 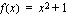 arvot ovat aina suurempia tai yhtäsuuria kuin yksi, koska luvun neliö on aina positiivinen tai nolla. Tämän funktion arvojoukko on siten
arvot ovat aina suurempia tai yhtäsuuria kuin yksi, koska luvun neliö on aina positiivinen tai nolla. Tämän funktion arvojoukko on siten 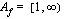 .
.
Testaa ensin oheisella testaa tietosi -tehtävällä, olitko ymmärtänyt, mikä on funktio.
Mitkä seuraavista säännöistä määrittelevät funktion joukolta 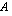 joukolle
joukolle 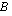 ?
?
Harjoittele sitten funktion tarkastelua oheisen oppimistehtävän sisältämän esimerkkifunktion avulla.
Oppimistehtävä 1.12.
Oppimistehtävä 1.13.
Muodosta annetun funktion lauseke muuttujan 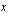 avulla.
avulla.
(a) Muodosta funktio 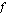 , joka ilmoittaa, kuinka henkilön nettopalkka riippuu bruttopalkasta
, joka ilmoittaa, kuinka henkilön nettopalkka riippuu bruttopalkasta 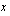 , kun ennakonpidätys on 22 %, eläke- ja työttömyysvakuutusmaksu 4,8 % ja ammattiyhdistyksen jäsenmaksu 1,2 %.
, kun ennakonpidätys on 22 %, eläke- ja työttömyysvakuutusmaksu 4,8 % ja ammattiyhdistyksen jäsenmaksu 1,2 %.
(b) Yritys on vuokrannut kopiokoneen firmasta, joka veloittaa 250 euroa kuukaudessa sekä lisäksi 3 senttiä/kopio. Muodosta funktio 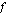 , joka ilmoittaa kopiokoneen kokonaisvuokran kuukaudessa koneella otetun kopiomäärän
, joka ilmoittaa kopiokoneen kokonaisvuokran kuukaudessa koneella otetun kopiomäärän 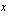 funktiona.
funktiona.
(c) Muodosta sitten funktio, joka ilmoittaa otettujen kopioiden yksikkökustannukset koneella otetun kopiomäärän 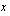 funktiona.
funktiona.
(d) Kun nelihenkisen perheen tulot ovat enemmän kuin 1268 euroa ja korkeintaan 3610 euroa, kunnan yhdestä lapsesta perimä päivähoitomaksu on 7,9 % em. tulorajan ylittävistä tuloista. Muodosta funktio, joka ilmoittaa perheeltä veloitetun päivähoitomaksun/muksu perheen kuukausitulojen 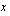 funktiona.
funktiona.
1.7.2. Funktion kuvaaja
Havainnollisen kuvan funktion kulusta ja sen kuvaamasta suureiden välisestä riippuvuudesta saa funktion kuvaajan avulla. Funktion kuvaaja muodostuu pisteistä 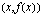 , missä
, missä 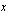 kuuluu funktion määrittelyjoukkoon
kuuluu funktion määrittelyjoukkoon 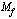 . Funktion kuvaajan pisteen
. Funktion kuvaajan pisteen 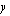 -koordinaatti ilmoittaa siis funktion arvon kyseisellä
-koordinaatti ilmoittaa siis funktion arvon kyseisellä 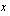 :n arvolla. Jos funktion
:n arvolla. Jos funktion 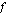 kuvaajalla on esimerkiksi piste
kuvaajalla on esimerkiksi piste 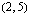 , tiedetään, että pisteessä 2 funktion arvo on 5 eli
, tiedetään, että pisteessä 2 funktion arvo on 5 eli 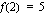 .
.
Seuraavan oppimistehtävän avulla voit harjoitella funktion kuvaajan tulkitsemista.
Oppimistehtävä 1.14.
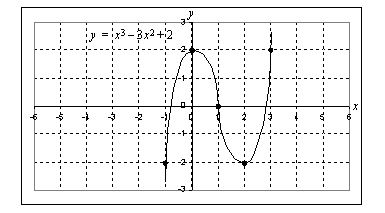
Ohessa on erään funktion 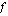 kuvaaja. Ratkaise seuraavat tehtävät tämän kuvaajan avulla.
kuvaaja. Ratkaise seuraavat tehtävät tämän kuvaajan avulla.
(b) Millä muuttujan arvoilla funktio saa arvon nolla?
(c) Mitkä luvut  toteuttavat yhtälön
toteuttavat yhtälön 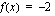 ?
?
(d) Arvioi, mitkä luvut toteuttavat yhtälön 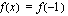 .
.
Ainakin ennen graafisten laskimien yleistymistä oppilaat usein karttoivat funktion kuvaajan piirtämistä. Työlästä se toki voi olla, mutta jos pystyt laskimella laskemaan funktion arvoja eri pisteissä, ei sen kuvaajan piirtämisessä pitäisi olla mitään ongelmaa. Seuraava esimerkki näyttäköön, kuinka saat funktion kuvaajan piirrettyä esimerkkipisteiden avulla.
Esimerkki 1.15.
Määrätään ensin taulukoimalla funktion kuvaajalta joitakin pisteitä, joiden avulla varsinainen kuvaaja piirretään. On siis laskettava ensin funktion arvoja muutamilla muuttujan 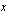 arvoilla.
arvoilla.
Tutustumme myöhemmin moniin eri funktiotyyppeihin ja niiden kuvaajiin. Tämän johdantojakson aikana on hyvä oppia yksinkertaisimman ja yleisimmän polynomifunktion eli ensimmäisen asteen polynomifunktion kuvaajan piirtäminen. Ensimmäisen asteen polynomifunktio on muotoa
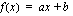 , missä vakiot
, missä vakiot 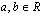 .
.
Esimerkiksi 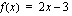 ja
ja 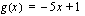 ovat ensimmäisen asteen polynomifunktioita. Ensimmäisen asteen polynomifunktion kuvaaja on suora. Suoran piirtämiseksi siltä on tiedettävä vähintään kaksi pistettä. Voit aina laskea nuo pisteet samaan tapaan kuin edellisessä esimerkissä. Itse kuitenkin piirrän suoran yleensä seuraavasti:
ovat ensimmäisen asteen polynomifunktioita. Ensimmäisen asteen polynomifunktion kuvaaja on suora. Suoran piirtämiseksi siltä on tiedettävä vähintään kaksi pistettä. Voit aina laskea nuo pisteet samaan tapaan kuin edellisessä esimerkissä. Itse kuitenkin piirrän suoran yleensä seuraavasti:
- Vakiotermi
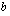 ilmoittaa pisteen, jossa suora leikkaa
ilmoittaa pisteen, jossa suora leikkaa 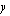 -akselin. Tiedetään, että
-akselin. Tiedetään, että 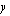 -akselilla
-akselilla 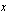 -koordinaatti on nolla, joten sijoittamalla
-koordinaatti on nolla, joten sijoittamalla 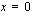 suoran yhtälöön saadaan
suoran yhtälöön saadaan 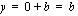 eli suora kulkee piteen
eli suora kulkee piteen 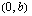 kautta. Näin löydetään helposti yksi suoran piste.
kautta. Näin löydetään helposti yksi suoran piste. - Suoran kulmakerroin
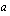 ilmoittaa suoran kaltevuuden. Jos esimerkiksi suoran kulmakerroin on 3, saadaan sen pisteitä kulkemalla aina yhdestä tunnetusta suoran pisteestä yksi askel oikealle ja 3 ylöspäin. Vastaavasti, jos suoran kulmakerroin on -0,5, saadaan sen pisteitä kulkemalla tunnetusta pisteestä aina yksi askel oikealle ja 0,5 askelta alaspäin (tai vastaavasti kaksi askelta oikealle ja 1 alaspäin). Suoran
ilmoittaa suoran kaltevuuden. Jos esimerkiksi suoran kulmakerroin on 3, saadaan sen pisteitä kulkemalla aina yhdestä tunnetusta suoran pisteestä yksi askel oikealle ja 3 ylöspäin. Vastaavasti, jos suoran kulmakerroin on -0,5, saadaan sen pisteitä kulkemalla tunnetusta pisteestä aina yksi askel oikealle ja 0,5 askelta alaspäin (tai vastaavasti kaksi askelta oikealle ja 1 alaspäin). Suoran 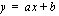 lisäpisteiden määrittäminen kulmakertoimen avulla tapahtuu siis aina niin, että tunnetusta suoran pisteestä (esim.
lisäpisteiden määrittäminen kulmakertoimen avulla tapahtuu siis aina niin, että tunnetusta suoran pisteestä (esim. 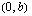 ) kuljetaan yhtä oikealle suuntautunutta siirtymää kohti kulmakeroimen
) kuljetaan yhtä oikealle suuntautunutta siirtymää kohti kulmakeroimen 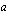 verran ylös- tai alaspäin kulmakertoimen etumerkistä riippuen.
verran ylös- tai alaspäin kulmakertoimen etumerkistä riippuen. 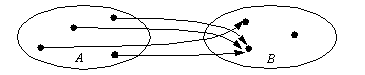
 ,
,  ,
, 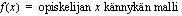 .
. 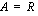 ,
, 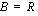 ,
, 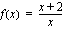 .
.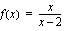 .
. 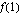 ja
ja 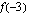
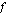 on määritelty?
on määritelty?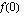 ,
, 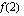 ja
ja 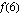
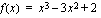 kuvaaja.
kuvaaja. 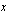
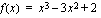
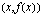
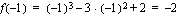
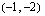
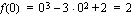
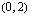
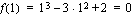
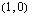
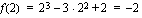
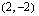
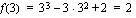
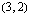
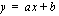 .
. 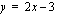 ,
, 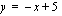 ja
ja 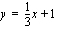 .
.