Vastaus:
Kun suoritukselle kertyvä yhden jakson korkokanta on desimaalilukuna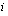 
, tulee suoritus aina yhden jakson aikana 
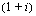-kertaiseksi. Viimeinen suoritus ei ole ehtinyt kasvaa korkoa, joten sen loppuarvo on 
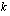. Toiseksi viimeinen suoritus on kasvanut korkoa yhden jakson, jolloin sen loppuarvo on 
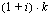. Kolmanneksi viimeinen suoritus on kasvanut korkoa kahden jakson ajan ja sen loppuarvo on 
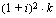. Erillisten suoritusten loppuarvot muodostavat geometrisen jonon, jonka ensimmäinen jäsen on 
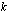, kahden peräkkäisen jäsenen suhdeluku 
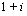ja jäsenten lukumäärä on 
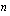. Geometrisen summan kaavalla näiden jaksollisten suoritusten yhteinen loppuarvo välittömästi viimeisen suorituksen tapahduttua on
.
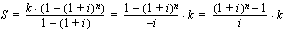