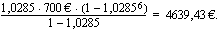[edellinen] [sisällys] [seuraava]
1.3. Geometrinen jono ja summa
1.3.1. Geometrinen jono
Lukujono on geometrinen, jos sen minkä tahansa kahden peräkkäisen jäsenen suhde (osamäärä) on vakio eli
Testaa tietosi III
Muodostetaan geometrinen lukujono, kun sen ensimmäinen jäsen on 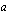 ja kahden peräkkäisen jäsenen suhde (
ja kahden peräkkäisen jäsenen suhde (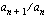 ) on
) on 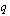 . Näiden tietojen perusteella voidaan muodostaa koko lukujono.
. Näiden tietojen perusteella voidaan muodostaa koko lukujono.
Esimerkki 1.9.
Geometrisen jonon ensimmäinen jäsen on 1,5 ja suhdeluku 1,2. Määrää jonon 28. jäsen. Anna vastaus kolmen desimaalin tarkkuudella.
Esimerkki 1.10.
Henkilö talletti vuoden alussa 4200 euroa tilille, jonka korkokanta on 2 %/vuosi. Korko liitetään pääomaan aina vuoden kuluttua, jolloin myös peritään 29 %:n suuruinen lähdevero korosta. Kuinka paljon tilillä on rahaa korkoineen kuuden vuoden kuluttua olettaen, että lisätalletuksia ei tehdä, lähdevero ei muutu eikä tililtä nosteta tuona aikana korkoja eikä muitakaan varoja?
Pääoma kasvaa tilillä korkoa 2 % vuodessa, mutta tästä korosta menee 29 % lähdeveroa. Tällöin asiakkaalle jää 71 % bruttokorosta eli hänen saamansa nettokorkokanta on
Tilin pääoma tulee siis vuosittain 1,0142-kertaiseksi. Lasketaan tilin kasvanut pääoma ensimmäisinä vuosina.
1.3.2. Geometrinen summa
Geometrisella summalla tarkoitetaan geometrisen jonon 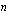 ensimmäisen jäsenen summaa (merkitään tunnuksella
ensimmäisen jäsenen summaa (merkitään tunnuksella 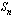 ). Edellä käytettyjä merkintöjä käyttäen geometrinen summa on
). Edellä käytettyjä merkintöjä käyttäen geometrinen summa on
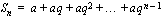 .
.
Johdetaan kaava geometrisen summan laskemiseksi. Kerrotaan edellä esitetty geometrisen summan yhtälö puolittain suhdeluvulla 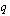 . Asetetaan nämä yhtälöt alekkain.
. Asetetaan nämä yhtälöt alekkain.
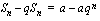 .
.
Ratkaistaan geometrinen summa 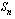 tästä yhtälöstä. Otetaan ensin yhtälön vasemmalla puolella yhteiseksi tekijäksi
tästä yhtälöstä. Otetaan ensin yhtälön vasemmalla puolella yhteiseksi tekijäksi 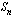 ja oikealla puolella
ja oikealla puolella 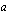 . Tämän jälkeen yhtälö tulee muotoon
. Tämän jälkeen yhtälö tulee muotoon
Jos geometrisen summan yhteenlaskettavien lukumäärä on 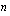 , ensimmäinen yhteenlaskettava on
, ensimmäinen yhteenlaskettava on 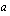 ja suhdeluku eli geometrisen jonon minkä tahansa kahden peräkkäisen jäsenen suhde
ja suhdeluku eli geometrisen jonon minkä tahansa kahden peräkkäisen jäsenen suhde 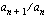 on
on 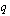 , niin geometrinen summa
, niin geometrinen summa 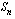 on
on
Esimerkki 1.12.
Määrää geometrisen jonon 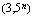 termien summa, kun
termien summa, kun 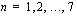 . Anna vastaus kahden desimaalin tarkkuudella.
. Anna vastaus kahden desimaalin tarkkuudella.
Esimerkki 1.13.
Matti talletti kuutena peräkkäisenä vuonna jokaisen vuoden alussa 700 euroa tilille, jonka veroton korkokanta oli 2,85 %/vuosi. Tilillä korko liitettiin pääomaan aina vuoden lopussa. Kuinka paljon Matin tilillä oli rahaa korkoineen kuudennen vuoden lopussa, kun tililtä ei tänä aikana nostettu varoja?
Ensimmäinen talletus oli kasvanut kuudennen vuoden loppuun mennessä korkoa kuusi vuotta eli siitä saatu kasvanut pääoma oli 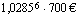 . Toinen talletus oli kasvanut korkoa viisi vuotta ja tullut korkoineen summaksi
. Toinen talletus oli kasvanut korkoa viisi vuotta ja tullut korkoineen summaksi 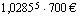 . Yhteensä talletukset olivat korkoineen kuudennen vuoden lopussa
. Yhteensä talletukset olivat korkoineen kuudennen vuoden lopussa
Oppimistehtävä 1.14.
Saat heinäkuuksi kesätyöpaikan. Työnantajan kysyttyä palkkatoivomustasi selität: "Haluan ensimmäiseltä päivältä 0,5 senttiä, toiseltä päivältä yhden sentin, kolmannelta kaksi, neljänneltä neljä senttiä jne. eli haluan palkkaa joka päivä kaksinkertaisen summan edelliseen päivään verrattuna." Kuinka suuri olisi heinäkuun palkkasi, jos työnantajasi suostuisi ehdotukseesi? Heinäkuussa on 23 työpäivää.
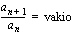 kaikilla
kaikilla 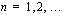
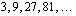 muodostavat geometrisen lukujonon, jonka kahden peräkkäisen jäsenen suhde on 3.
muodostavat geometrisen lukujonon, jonka kahden peräkkäisen jäsenen suhde on 3. 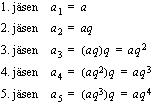
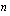 . jäsen on
. jäsen on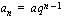 .
.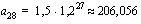 .
.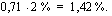
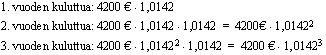
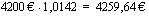 ja suhdeluku 1,0142. Kuuden vuoden kuluttua tilin saldo on
ja suhdeluku 1,0142. Kuuden vuoden kuluttua tilin saldo on 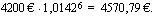
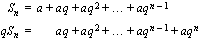
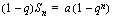 .
.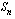 ratkeaa nyt yhtälöstä jamalla se puolittain tämän kertoimella
ratkeaa nyt yhtälöstä jamalla se puolittain tämän kertoimella 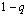 :
: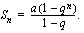
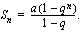
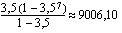 .
.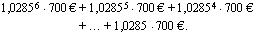
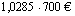 , suhdeluku on 1,0285 ja termien lukumäärä 6. Geometrisen summan kaavan avulla saadaan tilin kokonaissaldoksi kuudennen vuoden lopussa
, suhdeluku on 1,0285 ja termien lukumäärä 6. Geometrisen summan kaavan avulla saadaan tilin kokonaissaldoksi kuudennen vuoden lopussa