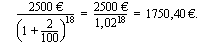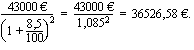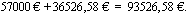[edellinen] [sisällys] [seuraava]
2.1. Kasvanut ja alkuperäinen pääoma
2.1.1. Kasvanut pääoma
Korko liitetään pääomaan kunkin korkojakson lopussa. Seuraavan jakson aikana myös tämä korko kasvaa korkoa. Opetellaan aluksi määrittämään kasvanut pääoma tapauksessa, jossa alkuperäinen pääoma kasvaa korkoa useita korkojaksoja. Otetaan käyttöön merkinnät:
Määrätään kasvanut pääoma kunkin korkojakson lopussa. Otetaan käyttöön alaindeksit, joilla ilmoitetaan, minkä korkojakson päätyttyä kyseinen kasvanut pääoma on laskettu. Lasketaan ensin 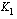 eli kasvanut pääoma ensimmäisen korkojakson päätyttyä. Korkokanta
eli kasvanut pääoma ensimmäisen korkojakson päätyttyä. Korkokanta 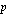 %/korkojakso ilmoittaa, kuinka monta prosenttia korkojakson korko on pääomasta. Kun ensimmäisen korkojakson korko liitetään pääomaan, on kasvanut pääoma
%/korkojakso ilmoittaa, kuinka monta prosenttia korkojakson korko on pääomasta. Kun ensimmäisen korkojakson korko liitetään pääomaan, on kasvanut pääoma 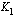 :
:
Kun tästä lausekkeesta otetaan alkuperäinen pääoma 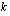 yhteiseksi tekijäksi, saadaan kasvanut pääoma muotoon
yhteiseksi tekijäksi, saadaan kasvanut pääoma muotoon
eli yhden korkojakson aikana pääoma kasvaa 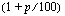 -kertaiseksi.
-kertaiseksi.
Käytetään tätä havaintoa hyväksi jatkossa ja muodostetaan taulukko, jossa seurataan pääoman kasvamista useiden korkojaksojen jälkeen.
Kun siis alkuperäinen pääoma  on kasvanut korkoa korkokannan
on kasvanut korkoa korkokannan 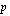 %/korkojakso mukaan
%/korkojakso mukaan 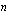 korkojaksoa, on kasvanut pääoma
korkojaksoa, on kasvanut pääoma 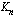 :
:
Esimerkki 2.1.
Laske kasvanut pääoma, kun 2000 euroa talletetaan 5 vuodeksi tilille, jonka veroton korkokanta on 2 %/vuosi. Tilillä korko liitetään pääomaan aina vuoden kuluttua.
Esimerkki 2.2.
Isovanhemmat tallettivat lapsenlapselleen 26.4.1980 15000 mk verottomalle tilille, jonka korkokanta oli 5,5 %/vuosi. Tilillä korko liitettiin pääomaan aina vuoden lopussa. Tili lopetettiin 26.4.1990, jolloin nostettiin kaikki sinne kertyneet varat. Kuinka paljon tilillä tuolloin oli rahaa, kun oletetaan, että korkokanta pysyi koko ajan samana eikä tililtä kyseisenä aikana nostettu varoja? Käytetään saksalaista korkoajanlaskua (kuukaudessa 30 pv, vuodessa 360 pv).
Lasketaan ensin, kuinka paljon tilille kertyy korkoa vuoden 1980 lopussa. Korkoaika 26.4.1980 - 31.12.1980 on saksalaisen korkoajanlaskun mukaan
Vuoden 1980 lopussa kasvanut pääoma oli 15559,17 mk. Tämä summa kasvoi korkoa vuoden 1989 loppuun mennessä yhteensä 9 korkojaksoa. Kasvanut pääoma oli 31.12.1989 yhteensä
Oppimistehtävä 2.3.
Laske kasvanut pääoma, kun 5800 euroa talletetaan 4 vuodeksi tilille, jonka lähdeverollinen korkokanta on 2,75 %/vuosi. Korko liitetään pääomaan aina vuoden kuluttua. Oletetaan, että lähdevero on koko ajan 29 %. (Vihje: laske nettokorkokanta vähentämällä lähdevero bruttokorkokannasta.)
2.1.2. Alkuperäinen pääoma
Tarkastellaan seuraavaksi käänteistä ongelmaa. Kuinka suuri alkuperäinen pääoma 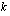 tuottaa
tuottaa 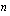 korkojakson aikana korkokannan
korkojakson aikana korkokannan 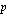 %/korkojakso mukaan kasvaneen pääoman
%/korkojakso mukaan kasvaneen pääoman 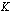 ? Tämä alkuperäinen pääoma
? Tämä alkuperäinen pääoma 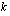 voidaan ratkaista edellä johdetusta koronkorkokaavasta
voidaan ratkaista edellä johdetusta koronkorkokaavasta
Tästä yhtälöstä alkuperäinen pääoma 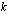 ratkeaa jakamalla yhtälö puolittain tämän tuntemattoman kertoimella
ratkeaa jakamalla yhtälö puolittain tämän tuntemattoman kertoimella 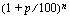 , jolloin saadaan
, jolloin saadaan
Esimerkki 2.4.
Kuinka suuri summa pitäisi sijoittaa verottomalle tilille, jonka korkokanta on 2 %/vuosi, jotta tilillä olisi korkoineen 18 vuoden kuluttua 2500 euroa? Oletetaan, että tilin korkokanta pysyy muuttumattomana koko ajan ja että tilillä korko liitetään pääomaan aina vuoden kuluttua.
Alkuperäisen pääoman määrittämistä käytetään myös erilaisten maksuvaihtoehtojen vertailuun. Kun maksuvaihtoehdot sisältävät eri suuruisia summia, jotka maksetaan vielä eri aikoina, saadaan nämä vaihtoehdot vertailukelpoisiksi laskemalla niiden kokonaisarvo samana ajankohtana. Jos ajankohdaksi valitaan esimerkiksi kaupantekohetki, lasketaan myöhemmin erääntyvien maksujen arvo tällä hetkellä määräämällä maksun suuruista kasvanutta pääomaa vastaava alkuperäinen pääoma.
Esimerkki 2.5.
Mitä kaupantekohetkellä maksettavaa kokonaissummaa 8,5 %:n vuotuisen korkokannan mukaan vastaa seuraava ostotarjous:
maksetaan 57000 euroa kaupantekohetkellä ja 43000 euroa kahden vuoden kuluttua? Anna vastaus kymmenen euron tarkkuudella.
Oppimistehtävä 2.6.
Yritys on saanut kiinteistön hankintaan kaksi maksuvaihtoehtoa:
(1) 580000 euroa kaupantekohetkellä tai
(2) 230000 euroa kaupantekohetkellä, 150000 euroa vuoden kuluttua ja 210000 euroa kahden vuoden kuluttua.
Kumpi maksuvaihtoehto on yritykselle edullisempi, kun vertailussa käytetään 8,5 %:n vuotuista korkokantaa?

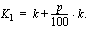
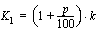
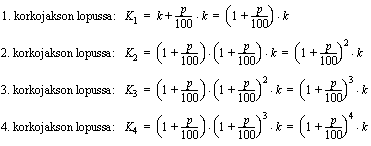
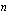 korkojakson kuluttua kasvanut pääoma on
korkojakson kuluttua kasvanut pääoma on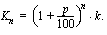
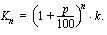
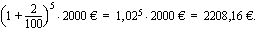
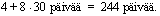
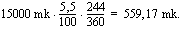
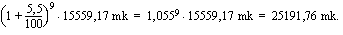
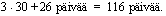
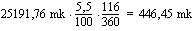
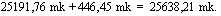
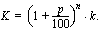
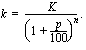
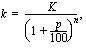
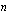 korkojakson aikana korkokannan
korkojakson aikana korkokannan 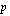 %/jakso mukaan saataisiin kasvanut pääoma
%/jakso mukaan saataisiin kasvanut pääoma 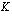 .
.