[edellinen] [sisällys] [seuraava]
4.2. Jatkuvuus
Ennen kuin voimme jatkaa derivaatan pariin, meidän on vielä selvitettävä, mitä tarkoitetaan funktion jatkuvuudella.
4.2.1. Jatkuvuuden määritelmä
Funktion sanotaan olevan jatkuva, jos sen kuvaaja on yhtenäinen, katkeamaton käyrä. Funktio on epäjatkuva kohdassa, jossa sen kuvaaja katkeaa. Tämä havainnollinen kuvaus funktion jatkuvuudesta ei vielä kelpaa jatkuvuuden määritelmäksi. Vastaa seuraavan oppimistehtävän kysymyksiin. Sen avulla voit oivaltaa, mitä funktiolta edellytetään, jotta se olisi jatkuva tietyssä kohdassa eli jotta sen kuvaaja ei katkeaisi kyseisessä kohdassa.
Oppimistehtävä 3.2.
Seuraavassa linkit sivuille, joista löydät neljän eri funktion kuvaajat.
http://www.cc.jyu.fi/~anvihola/testit/lim/esim3.php
http://www.cc.jyu.fi/~anvihola/testit/lim/esim4.php
http://www.cc.jyu.fi/~anvihola/testit/lim/esim2.php
http://www.cc.jyu.fi/~anvihola/testit/lim/esim1.php
Näitä verkossa olevia esimerkkejä tutkiessasi voit liikutella 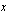 -akselilla kahta pistettä X1 ja X2 sekä nähdä samalla funktion arvon kyseisissä pisteissä.
-akselilla kahta pistettä X1 ja X2 sekä nähdä samalla funktion arvon kyseisissä pisteissä.
Täydennä alla oleva taulukko kuvien perusteella.
Edellisen oppimistehtävän tehtyäsi huomasit varmaan, että funktio oli jatkuva kohdassa 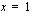 vasta silloin, kun sen vasemman- ja oikeanpuoleinen raja-arvo sekä funktion arvo kyseisessä kohdassa olivat yhtäsuuret. Toispuoleisten raja-arvojen yhtäsuuruus takaa sen, että funktiolla on raja-arvo kyseisessä kohdassa. Tällöin siis funktion arvot lähestyvät samaa lukua lähestyttiinpä kyseistä kohtaa oikealta tai vasemmalta. Tämä ei kuitenkaan riitä siihen, että funktio olisi jatkuva kyseisessä kohdassa. Funktiohan ei ole välttämättä edes määritelty kohdassa, jossa sillä on raja-arvo. Toisaalta vaikka funktio olisi määritelty kohdassa, jossa sillä on raja-arvo, voi se kuitenkin olla epäjatkuva kyseisessä kohdassa. Näin käy, jos funktion arvo ja raja-arvo ovat erisuuret tässä kohdassa.
vasta silloin, kun sen vasemman- ja oikeanpuoleinen raja-arvo sekä funktion arvo kyseisessä kohdassa olivat yhtäsuuret. Toispuoleisten raja-arvojen yhtäsuuruus takaa sen, että funktiolla on raja-arvo kyseisessä kohdassa. Tällöin siis funktion arvot lähestyvät samaa lukua lähestyttiinpä kyseistä kohtaa oikealta tai vasemmalta. Tämä ei kuitenkaan riitä siihen, että funktio olisi jatkuva kyseisessä kohdassa. Funktiohan ei ole välttämättä edes määritelty kohdassa, jossa sillä on raja-arvo. Toisaalta vaikka funktio olisi määritelty kohdassa, jossa sillä on raja-arvo, voi se kuitenkin olla epäjatkuva kyseisessä kohdassa. Näin käy, jos funktion arvo ja raja-arvo ovat erisuuret tässä kohdassa.
Funktio 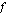 on siis jatkuva kohdassa
on siis jatkuva kohdassa 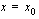 , jos sen vasemman- ja oikeanpuoleinen raja-arvo sekä funktion arvo ovat yhtäsuuret tässä kohdassa eli
, jos sen vasemman- ja oikeanpuoleinen raja-arvo sekä funktion arvo ovat yhtäsuuret tässä kohdassa eli
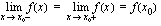 .
.
Ensimmäinen yhtäsuuruus takaa sen, että funktiolla 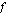 on raja-arvo kohdassa
on raja-arvo kohdassa 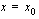 . Jälkimmäinen puolestaan takaa sen, että funktio
. Jälkimmäinen puolestaan takaa sen, että funktio 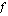 on määritelty kyseisessä kohdassa ja että sen arvo on sama kuin funktion raja-arvo tässä kohdassa. Jotta funktio
on määritelty kyseisessä kohdassa ja että sen arvo on sama kuin funktion raja-arvo tässä kohdassa. Jotta funktio 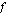 olisi jatkuva kohdassa
olisi jatkuva kohdassa 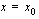 , on funktiolla oltava raja-arvo tässä kohdassa, funktion on oltava määritelty tässä kohdassa ja funktion arvon sekä raja-arvon on oltava yhtäsuuret kyseisessä kohdassa. Jatkuvuuden määritelmä esitetäänkin usein näin: funktio
, on funktiolla oltava raja-arvo tässä kohdassa, funktion on oltava määritelty tässä kohdassa ja funktion arvon sekä raja-arvon on oltava yhtäsuuret kyseisessä kohdassa. Jatkuvuuden määritelmä esitetäänkin usein näin: funktio 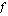 on jatkuva kohdassa
on jatkuva kohdassa 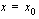 , jos
, jos
4.2.2. Bolzanon lause
Jatkuvilla funktioilla on monia tärkeitä ominaisuuksia. Tässä yhteydessä mainittakoon ns. Bolzanon lause, jonka mukaan suljetulla välillä jatkuva funktio ei voi vaihtaa merkkiään käymättä välillä nollassa. Geometrisesti tukittuna tämä tarkoittaa sitä, että jatkuvan funktion kuvaaja ei voi kulkea 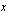 -akselin puolelta toiselle leikkaamatta välillä tätä akselia ainakin yhdessä pisteessä. Bolzanon lausetta voidaan hyödyntää mm. etsittäessä yhtälölle likimääräistä ratkaisua. Tällöin yhtälö muutetaan muotoon, jossa haetaan jonkun jatkuvan funktion nollakohtia. Kun löydetään kohdat, joissa funktion arvot ovat erimerkkiset, tiedetään, että näiden kohtien välissä on ainakin yksi kohta, jossa funktio saa arvon nolla. Tälle nollakohdalle saadaan aina tarkempia likiarvoja esimerkiksi puolittamalla ratkaisuväli systemaattisesti ja tarkistamalla aina, kummalla puoliskolla nollakohta on. Näin jatketaan, kunnnes ratkaisuväli on kavennettu halutulle tarkkuudelle.
-akselin puolelta toiselle leikkaamatta välillä tätä akselia ainakin yhdessä pisteessä. Bolzanon lausetta voidaan hyödyntää mm. etsittäessä yhtälölle likimääräistä ratkaisua. Tällöin yhtälö muutetaan muotoon, jossa haetaan jonkun jatkuvan funktion nollakohtia. Kun löydetään kohdat, joissa funktion arvot ovat erimerkkiset, tiedetään, että näiden kohtien välissä on ainakin yksi kohta, jossa funktio saa arvon nolla. Tälle nollakohdalle saadaan aina tarkempia likiarvoja esimerkiksi puolittamalla ratkaisuväli systemaattisesti ja tarkistamalla aina, kummalla puoliskolla nollakohta on. Näin jatketaan, kunnnes ratkaisuväli on kavennettu halutulle tarkkuudelle.
Bolzanon lause ja sen käyttö yhtälön likimääräisen ratkaisun etsimiseen on esitelty luentomonisteessa sivulla 135. Lue kyseinen kohta sekä katso esimerkki 5.7. Riittää, että ymmärrät idean, johon esimerkissä esitelty haarukointimenetelmä perustuu. Käytännössä yhtälön likimääräiseen ratkaisemiseen käytetään tietokoneohjelmia tai laskimia, joihin menetelmä on ohjelmoitu valmiiksi.
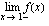
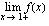
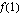
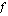 jatkuva kohdassa
jatkuva kohdassa 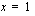 ?
? 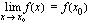 .
. 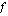 on epäjatkuva kohdassa
on epäjatkuva kohdassa 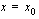 , jota kutsutaan tällöin funktion
, jota kutsutaan tällöin funktion 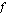 epäjatkuvuuskohdaksi.
epäjatkuvuuskohdaksi.