[edellinen] [sisällys] [seuraava]
3.5. Analyyttistä geometriaa
Olemme tällä kurssilla tutustuneet jo kahteen eri tasokäyrään: suoraan ja paraabeliin. Se matematiikan osa-alue, joka tutkii mm. erilaisia tasokäyriä on ns. analyyttinen geometria. Analyyttisen geometrian perustana on tason varustaminen koordinaatistolla. Tällöin tasokäyriä voidaan esittää kahden muuttujan yhtälöiden (esim. 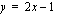 tai
tai 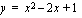 ) avulla. Käyrien ominaisuuksia tutkiminen muuttuu tällöin yhtälöiden tarkasteluksi. Esimerkiksi geometrisen perussuhteen "piste on käyrällä" korvaa anlyyttisessä geometriassa laskennollinen ehto "pisteen koordinaatit toteuttavat käyrän yhtälön".
) avulla. Käyrien ominaisuuksia tutkiminen muuttuu tällöin yhtälöiden tarkasteluksi. Esimerkiksi geometrisen perussuhteen "piste on käyrällä" korvaa anlyyttisessä geometriassa laskennollinen ehto "pisteen koordinaatit toteuttavat käyrän yhtälön".
Tässä osiossa opetellaan muutama uusia asia suoriin liittyen sekä tutustutaan aivan uuteen tasokäyrään eli ympyrään.
3.5.1. Suora
Olemme jo harjoitelleet suoran piirtämistä sen yhtälön avulla. Suoran piirtäminen onnistuu kätevästi, kun sen yhtälö on muokattu ns. ratkaistuun muotoon 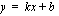 , missä vakio
, missä vakio 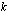 ilmoittaa suoran kulmakertoimen ja vakio
ilmoittaa suoran kulmakertoimen ja vakio 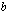 kohdan, jossa suora leikkaa
kohdan, jossa suora leikkaa 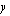 -akselin. Suoran yhtälö voidaan esittää myös ns. yleisessä muodossa
-akselin. Suoran yhtälö voidaan esittää myös ns. yleisessä muodossa 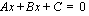 , missä ainakin toinen vakioista
, missä ainakin toinen vakioista 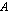 ja
ja 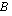 ovat nollasta poikkeavia. Esimerkiksi
ovat nollasta poikkeavia. Esimerkiksi 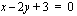 on suoran yhtälön yleinen muoto. Piirtämistä varten kyseinen yhtälö kannattaa muokata ratkaistuun muotoon ratkaisemalla
on suoran yhtälön yleinen muoto. Piirtämistä varten kyseinen yhtälö kannattaa muokata ratkaistuun muotoon ratkaisemalla 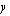 tästä yhtälöstä. Tällöin edellä mainittu yhtälö tulee muotoon
tästä yhtälöstä. Tällöin edellä mainittu yhtälö tulee muotoon 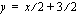 .
.
Suora on täysin määrätty, jos siltä tunnetaan yksi piste ja lisäksi tiedetään sen suunta eli tunnetaan suoran kulmakerroin. Seuraavaksi opetellaankin määrittämään suoran yhtälö tässä tapauksessa. Tätä varten on olemassa oma kaava, joka on johdettu luentomonisteen luvussa 3.1.1 sivulla 56. Kyseisen kaavan mukaan suoralla, joka kulkee pisteen 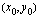 kautta ja jonka kulmakerroin on
kautta ja jonka kulmakerroin on 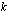 , on yhtälö
, on yhtälö
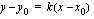 .
.
Lue kaavan johtaminen luentomonisteesta ja katso siihen liittyvä esimerkki 3.1. Lopuksi voit vielä harjoitella suoran yhtälön määrittämistä tällaisessa tilanteessa oheisen oppimistehtävän avulla.
Oppimistehtävä 3.19.
Määrää yhtälö suoralle, joka kulkee pisteen 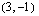 kautta ja jonka kulmakerroin on 2. Ilmoita yhtälö ratkaistussa muodossa.
kautta ja jonka kulmakerroin on 2. Ilmoita yhtälö ratkaistussa muodossa.
Lisäksi meidän on opeteltava määrittämään suoran kulmakerroin, kun suoralta tunnetaan kaksi pistettä. Suoran kulmakerroinhan ilmoittaa meille suoran suunnaan. Kun suora kulkee pisteiden 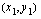 ja
ja 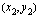 kautta, sen kulmakerroin
kautta, sen kulmakerroin 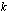 on
on
eli kulmakerroin saadaan jakamalla 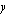 -koordinaattien erotus
-koordinaattien erotus 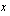 -koordinaattien erotuksella. Huomaa, että molemmat erotukset lasketaan aina samassa järjestyksessä (pisteen 2 koordinaateista vähennetään vastaavat pisteen 1 koordinaatit). Oheisella testaa tietosi -tehtävällä voit varmistaa, että osaat määrittää suoran kulmakertoimen sen kahden pisteen koordinaattien avulla.
-koordinaattien erotuksella. Huomaa, että molemmat erotukset lasketaan aina samassa järjestyksessä (pisteen 2 koordinaateista vähennetään vastaavat pisteen 1 koordinaatit). Oheisella testaa tietosi -tehtävällä voit varmistaa, että osaat määrittää suoran kulmakertoimen sen kahden pisteen koordinaattien avulla.
Testaa tietosi VII
Suora kulkee pisteiden 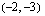 ja
ja 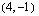 kautta. Mikä on suoran kulmakerroin?
kautta. Mikä on suoran kulmakerroin?
Nyt, kun osaamme määrittää suoran yhtälön silloin, kun siltä tiedetään yksi piste sekä kulmakerroin ja osaamme myös määrittää suoran kulmakertoimen sen kahden pisteen avulla, voimme tietysti määrittää suoran yhtälön silloin, kun siltä tunnetaan kaksi pistettä. Sijoitamme tuolloin vain edellä käytettyyn suoran yhtälön kaavaan kulmakertoimen paikalle kahden pisteen avulla lasketun kulmakertoimen. Kun suora kulkee pisteiden 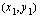 ja
ja 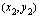 kautta, sen yhtälö on
kautta, sen yhtälö on
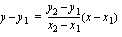 .
.
Lue nyt luentomonisteen luvusta 3.1.2 sivulta 57 alkaen, mitä siellä kerrotaan suoran kulmakertoimesta. Katso erityisesti esimerkit 3.2 ja 3.3. Lopuksi voit vielä harjoitella suoran yhtälön määrittämistä oheisen oppimistehtävän avulla.
3.5.2. Ympyrä
Luentomonisteessa on ympyrää esitelty luvussa 3.4. Lue sieltä ympyrän yhtälön johtaminen sekä esimerkki 3.7. Tämän luettuasi sinun pitäisi tietää, että ympyrällä, jonka keskipiste on 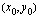 ja säde
ja säde 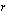 on yhtälö
on yhtälö
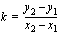
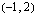 ja
ja 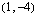 kautta. Mikä on suoran yhtälö? Ilmoita se ratkaistussa muodossa.
kautta. Mikä on suoran yhtälö? Ilmoita se ratkaistussa muodossa. 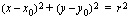 .
.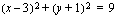 keskipiste on
keskipiste on 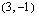 ja säde 3 ja ympyrän
ja säde 3 ja ympyrän 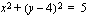 keskipiste on
keskipiste on 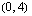 sekä säde
sekä säde 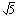 . Tällä kurssilla on tärkeintä, että osaat piirtää ympyrän koordinaatistoon sen yhtälön avulla. Tätä voit harjoitella oheisen oppimistehtävän avulla.
. Tällä kurssilla on tärkeintä, että osaat piirtää ympyrän koordinaatistoon sen yhtälön avulla. Tätä voit harjoitella oheisen oppimistehtävän avulla. 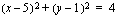 ja
ja 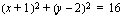 samaan koordinaatistoon.
samaan koordinaatistoon.