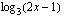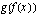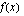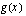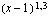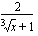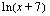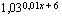[edellinen] [sisällys] [seuraava]
3.4. Yhdistetty funktio
Tarkastellaan funktiota 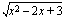 . Kun lasket tämän funktion arvoa esimerkiksi kohdassa
. Kun lasket tämän funktion arvoa esimerkiksi kohdassa 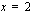 , suoritat sen kahdessa vaiheessa: lasket ensin muuttujan arvolla 2 juurrettavan arvon
, suoritat sen kahdessa vaiheessa: lasket ensin muuttujan arvolla 2 juurrettavan arvon
ja tämän jälkeen otat tuloksesta neliöjuuren ja saat funktion arvoksi kohdassa 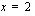 luvun
luvun 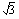 . Voimme tässä tapauksessa ajatella, että funktio
. Voimme tässä tapauksessa ajatella, että funktio 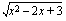 on yhdistetty kahdesta eri funktiosta: juurrettavassa olevasta polynomista
on yhdistetty kahdesta eri funktiosta: juurrettavassa olevasta polynomista 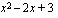 , jonka arvoon sovelletaan neliöjuurifunktiota
, jonka arvoon sovelletaan neliöjuurifunktiota 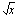 .
.
Voimme ajatella funktion kahdesta eri funktiosta yhdistetyksi funktioksi silloin, kun sen arvoa laskettaessa meidän on ensin laskettava yhden funktion arvo (em. polynomi) ja tämän funktion arvoon on vielä sovellettava jotakin toista funktiota (neliöjuuri johdantoesimerkissä). Oheisessa taulukossa on esimerkkejä yhdistetyista funktioista ja siitä ilmenee myös, mikä on se funktio, jonka arvo on laskettava ensin ja mikä on se toinen funktio, jota tuohon arvoon lopuksi sovelletaan.
Olkoot 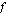 ja
ja 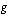 joitakin funktioita. Niistä muodostettu yhdistetty funktio
joitakin funktioita. Niistä muodostettu yhdistetty funktio 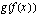 (luetaan "
(luetaan "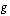 arvolla
arvolla 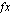 ") saadaan sijoittamalla funktion
") saadaan sijoittamalla funktion 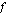 lauseke muuttujan paikalle funktion
lauseke muuttujan paikalle funktion 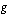 lausekkeeseen. Funktiota
lausekkeeseen. Funktiota 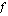 , jonka lauseke sijoitetaan muuttujan paikalle toiseen funktioon sanotaan sisäfunktioksi. Funktio
, jonka lauseke sijoitetaan muuttujan paikalle toiseen funktioon sanotaan sisäfunktioksi. Funktio 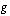 , jonka lausekeeseen muuttujan paikalle tuo sisäfunktio sijoitetaan, on puolestaan ulkofunktio. Seuraavassa esimerkissä harjoitellan funktioiden yhdistämistä.
, jonka lausekeeseen muuttujan paikalle tuo sisäfunktio sijoitetaan, on puolestaan ulkofunktio. Seuraavassa esimerkissä harjoitellan funktioiden yhdistämistä.
Esimerkki 3.18.
Olkoon sisäfunktio 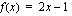 . Muodosta yhdistetty funktio
. Muodosta yhdistetty funktio 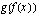 , kun ulkofunktio
, kun ulkofunktio 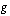 on
on
Seuraavassa modulissa tarvitsemme erityisesti taitoa tunnistaa yhdistetty funktio sekä sen sisä- ja ulkofunktio. Huomaa, että hajoitellessamme johdannossa funktion tunnistamista yhdistetyksi funktioksi löysimme jo sen sisä- ja ulkofunktion, vaikka emme noita nimityksiä vielä tienneetkään. Ajattelutapa, jota tuolloin käytettiin sopii mielestäni hyvin yhdistetyn funktion tunnistamiseen. Sen sisäfunktion löytää mukavasti miettimällä, minkä funktion arvo on laskettava ensin, ennen kuin funktion arvon tietyssä pisteessä saa selville. Ulkofunktio on puolestaan se funktio, jota tuohon arvoon sovelletaan. Kokeilepa nyt itse sisä- ja ulkofunktion löytämistä yhdistetystä funktiosta oheisen testaa tietosi -tehtävän avulla.
Vielä on syytä huomata, että funktio voidaan ajatella yhdistetyksi funktioksi monellakin tavalla. Edellä esitetyt tulkinnat ovat vain yksi vaihtoehto. Esimerkiksi funktio 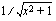 voidaan ajatella yhdisteyksi funktioksi
voidaan ajatella yhdisteyksi funktioksi 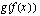 siten, että sisäfunktio
siten, että sisäfunktio 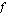 on
on 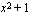 ja ulkofunktio
ja ulkofunktio 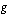 on
on 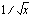 . Toinen tapa tulkita samainen funktio yhdistetyksi funktioksi on ajatella sisäfunktioksi
. Toinen tapa tulkita samainen funktio yhdistetyksi funktioksi on ajatella sisäfunktioksi 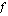 koko nimittäjä
koko nimittäjä 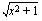 ja ulkofunktioksi
ja ulkofunktioksi 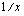 . Tässä yhteydessä olevien harjoitusten malliratkaisuissa olen näyttänyt vain yhden tavan tulkita funktiot yhdistetyiksi funktioiksi.
. Tässä yhteydessä olevien harjoitusten malliratkaisuissa olen näyttänyt vain yhden tavan tulkita funktiot yhdistetyiksi funktioiksi.
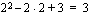
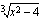
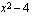
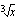
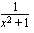
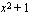
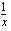
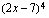
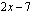
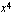
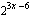
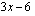
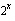
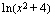
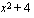
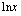
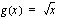 (b)
(b) 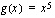
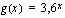 (d)
(d) 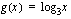
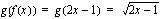
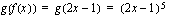
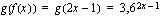
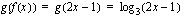
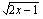 (b)
(b) 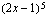 (c)
(c) 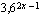 (d)
(d)