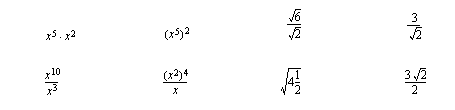[edellinen] [sisällys] [seuraava]
1.2. Itseisarvo, potenssi ja neliöjuuri
1.2.1. Itseisarvo
Reaaliluvun 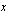 itseisarvolla, jota merkitään
itseisarvolla, jota merkitään 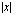 , tarkoitetaan luvun etäisyyttä nollasta lukusuoralla. Positiivisen luvun etäisyyden nollasta ilmaisee luku itse. Negatiivisen luvun etäisyyden nollasta ilmoittaa luvun vastaluku, joka on positiivinen. Luvun itseisarvo on siis aina positiivinen tai nolla, mikäli luku itse on nolla.
, tarkoitetaan luvun etäisyyttä nollasta lukusuoralla. Positiivisen luvun etäisyyden nollasta ilmaisee luku itse. Negatiivisen luvun etäisyyden nollasta ilmoittaa luvun vastaluku, joka on positiivinen. Luvun itseisarvo on siis aina positiivinen tai nolla, mikäli luku itse on nolla.
1.2.2. Potenssi
Kertaa potenssimerkintä ja potenssilaskusäännöt esimerkkeineen kurssimonisteesta. Jos nämä asiat ovat unohtuneet, harjoittele niitä oheisen oppimistehtävän avulla. Potenssikäsitettä laajennetaan myöhemmin tällä kurssilla modulissa 3. Silloin harjoitellaan lisää potenssilausekkeiden käsittelyä.
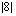 (b)
(b) 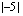 (c)
(c) 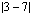 (d)
(d) 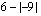
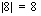
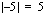
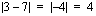
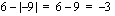
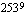 , saat laskimesi näyttöön tuloksen
, saat laskimesi näyttöön tuloksen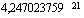 .
.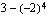 (ii)
(ii) 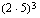 (iii)
(iii) 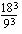
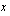 potenssina
potenssina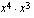 (ii)
(ii) 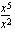 (iii)
(iii) 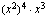
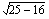 (b)
(b) 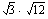 (c)
(c) 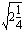
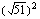 (e)
(e) 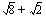 (f)
(f)